先生~。基礎のたすきがけの因数分解はできるようになったのですが、
\(x^2-xy-2y^2+2x-y+1\) の因数分解にてこずっています。
この式を眺めていても確かに解法は見つかりませんね。
まずは「1つの文字」について着目しましょう。
あっ!たしか最低次数の文字について整理するんですよね。
今回は\(x^2\) と \(y^2\) の次数が同じだから~
とりあえず \(x\) に着目して \(○x^2+△x+□\) の形に直してみます!
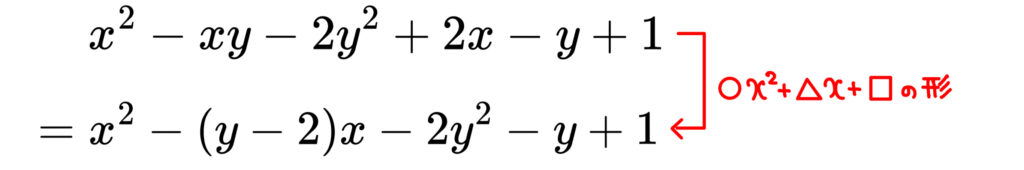
あとは2次式なので「たすきがけ」をすればよいわけですね。
まずは定数の部分も掛け算に直しておきましょう。
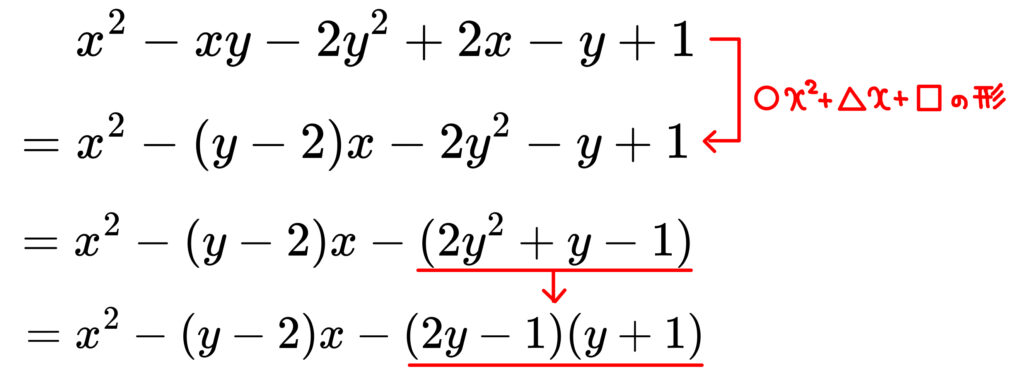
ここまでくれば、いままでやってきたたすきがけのように試行錯誤すればいいんですね!
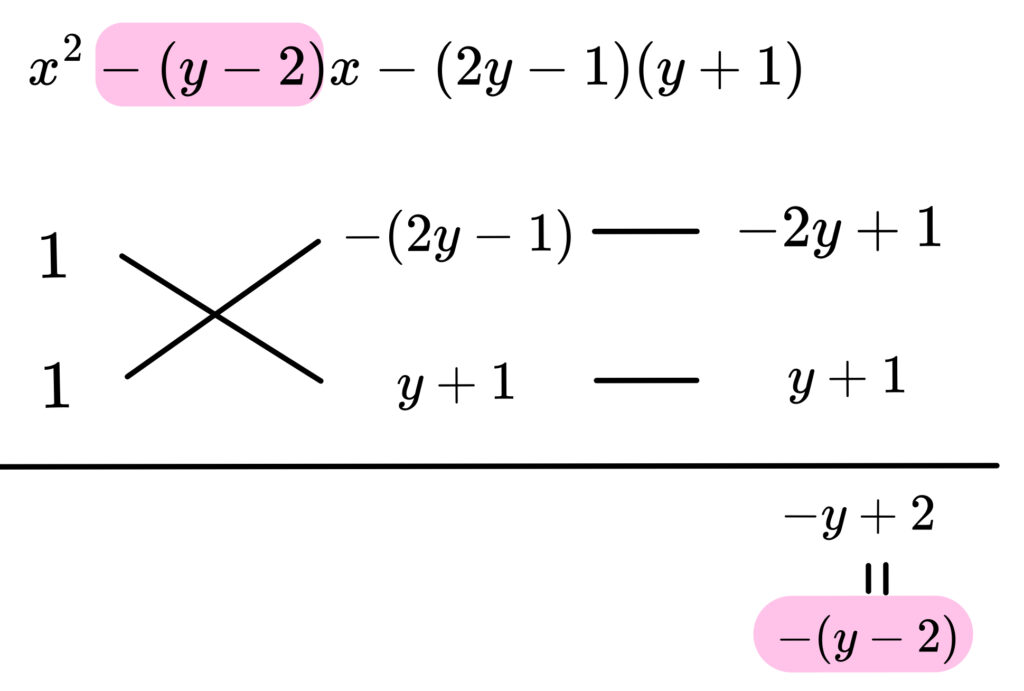
はい。そういうことですね。
因数分解の結果は \(\{x-(2y-1)\}\{x+(y+1)\}\)
つまり \((x-2y+1)(x+y+1)\) となります。
なんとなく自信がついてきました!
ではもう一問。
チャレンジしてみましょう!
問題
\(2x^2-5xy-3y^2+5x+13y-12\) を因数分解せよ。
これも\(x\) , \(y\) ともに2次式ですね。
じゃあとりあえず\(x\) に着目して整理してみると、、、
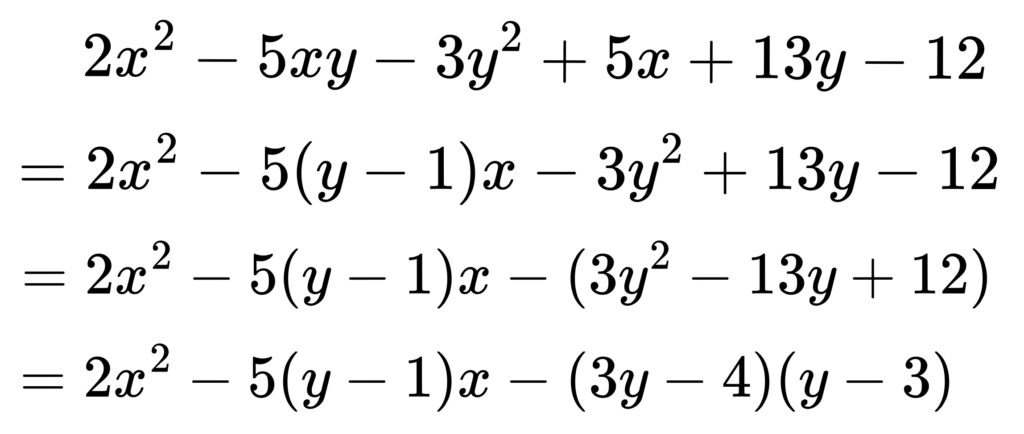
そこまでくれば、あともう一歩ですね。
うまくいけた気がします!

答えは\(\{2x+(y-3)\}\{x-(3y-4)\}\),
つまり、\((2x+y-3)(x-3y+4)\) ですね!
n浪君、大正解です。
これで完璧ですね。




コメント