先生~。今日は順列について教えてください。
そもそも順列ってなんですか?
順列というのは簡単に言うと、
文字などを一列に並べたときにできる列のことです。
ただそれだけなんですね…。
1つ順列に関する問題をやってみたいと思います!
問題
次の場合の数をそれぞれ求めよ。
\((1)~~A,B,C,D,E\) の5個の文字から3つ選んで、横1列に並べる方法は何通りあるか。
\((2)~~0\sim9\) の10個の文字を使って4桁のパスワードを作る方法は何通りあるか。
さぁn浪君。
まずは今まで学習したことを使って数えてみましょう。
\((1)\) はとりあえず樹形図を使って考えてみます。
えーと…。
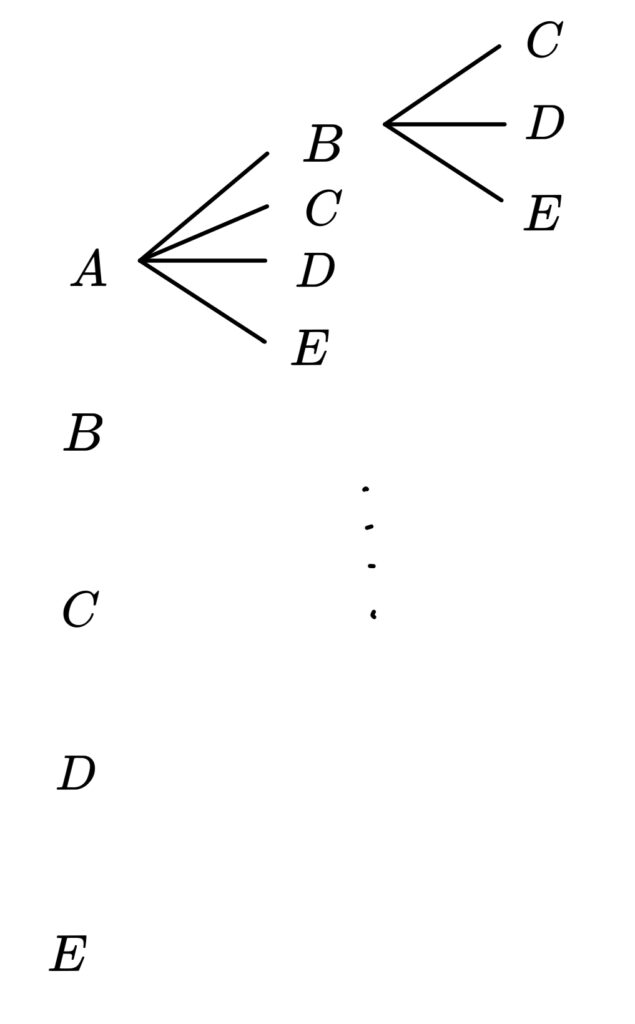
n浪君。考え方はOKです!
ですがこの樹形図、全部書くのは大変じゃないですか?
大変ですね…。
樹形図はもっとコンパクトに、このように書くといいでしょう。
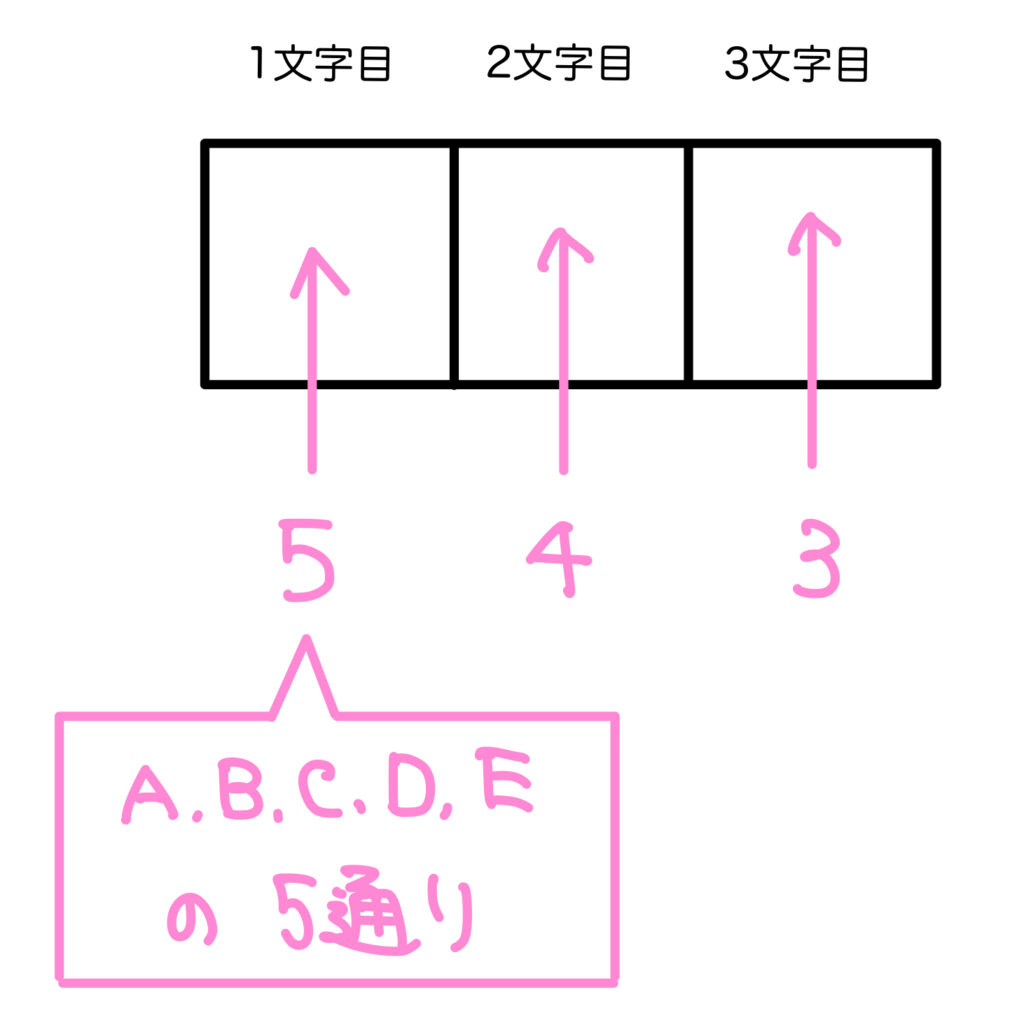
確かにこの書き方のほうがコンパクトですね!
ってことは、積の法則から\(5\times4\times3=60\) 通りですね。
では\((2)\) はどうでしょう?
\((1)\) と同じじゃないですか~。
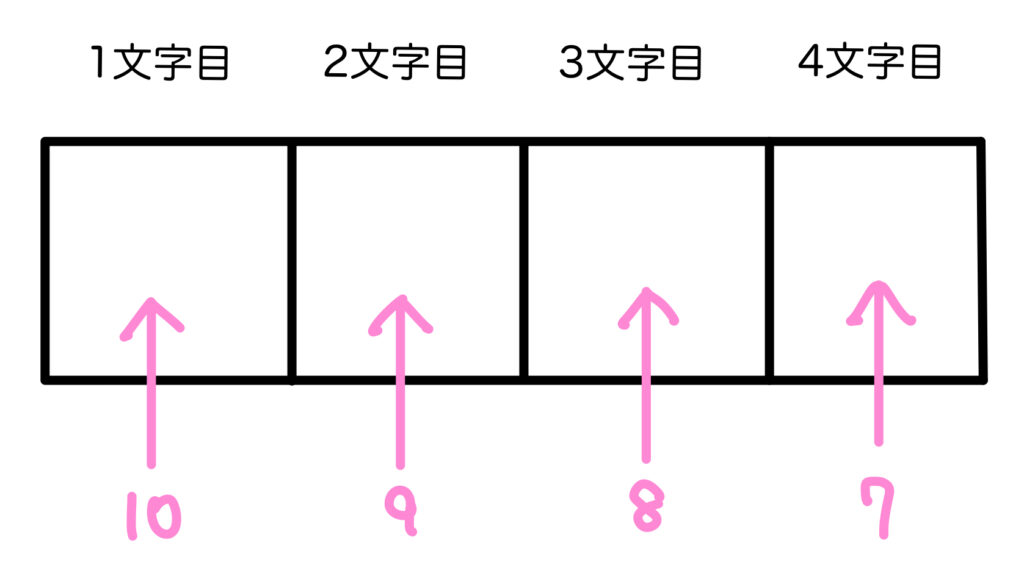
ちょっと待ってください。
パスワードなら基本は同じ文字は使用可能ですよ?
そっか!たしかに4桁のパスワードなら1111もOKか…。
じゃあ改めてやってみると…
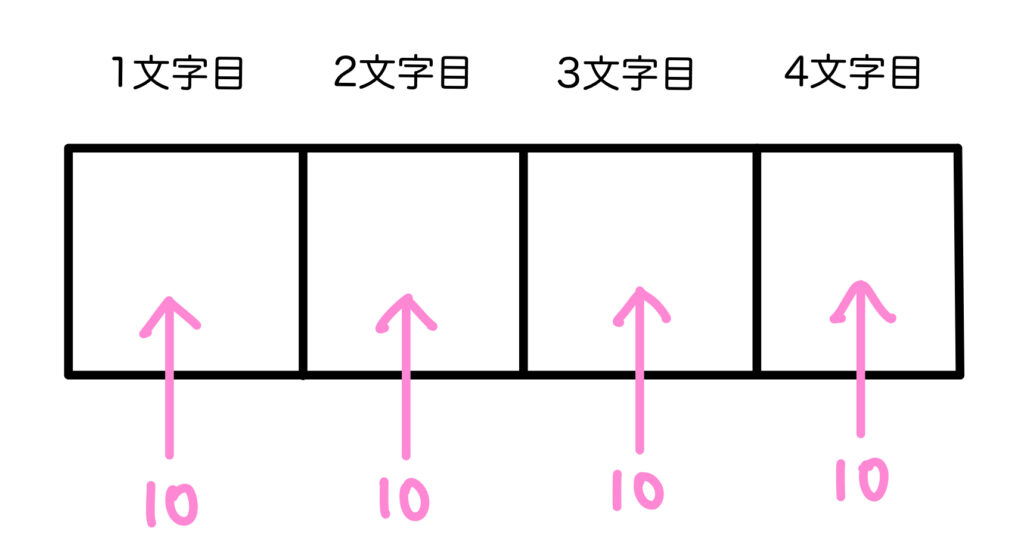
これも積の法則から,
\(10\times10\times10\times10=10000\) 通りです!
正解です。
これは後で学ぶ重複順列というものなんですが、
重要なのは順列は樹形図を考えることで簡単に計算できるんです。
なるほど~。
樹形図のコンパクトな書き方も知れてよかったです!
さぁ次は、順列の記号 \(_n\mathrm{P}_r\) について学びましょう。




コメント