先生!今日は円順列とじゅず順列について教えてください!
わかりました。
n浪君。まずは教科書にはどう書いてあるでしょう?
こんなことが書いてあるページを発見しました!
1.異なる \(n\) 個のものの円順列の総数は \((n-1)!\)
2.異なる \(n\) 個のもののじゅず順列の総数は \(\dfrac{(n-1)!}{2}\)
確かに書いてありますね。
でも実はこれは覚えてほしくない公式です。
えっ!これを覚えておけば簡単に解けると思ったのに…。
先生、なんで覚えちゃいけないんですか?
公式を使うだけで解ける問題はほとんどありません。
ですから、ちゃんと理解して応用が利くようにしておきましょう。
では1つ初歩の問題で公式を理解しましょう。
\((1)~~\)色の異なる6個の玉を円形に並べる方法は何通りあるか。
\((2)~~\)色の異なる6個の玉を糸でつないで首飾りにする方法は何通りあるか。
\((1)\) が円順列、\((2)\) がじゅず順列の問題ですね。
どうやって考えるんでしょう?
まず円順列について、通常の順列と異なるのは
回転すると同一視できる並びが存在することですね。

じゃあ余計に数えてしまわないように工夫が必要ですね…
はい。私がオススメするのは
「どこか1つから見える景色が何パターンあるか」
という考え方です。
景色が何パターンあるか?
もうすこし解説してください!
では、例えば赤玉からの景色を考えるとしましょう。
すると赤玉からは5個の玉が並んでいるように見えますね。
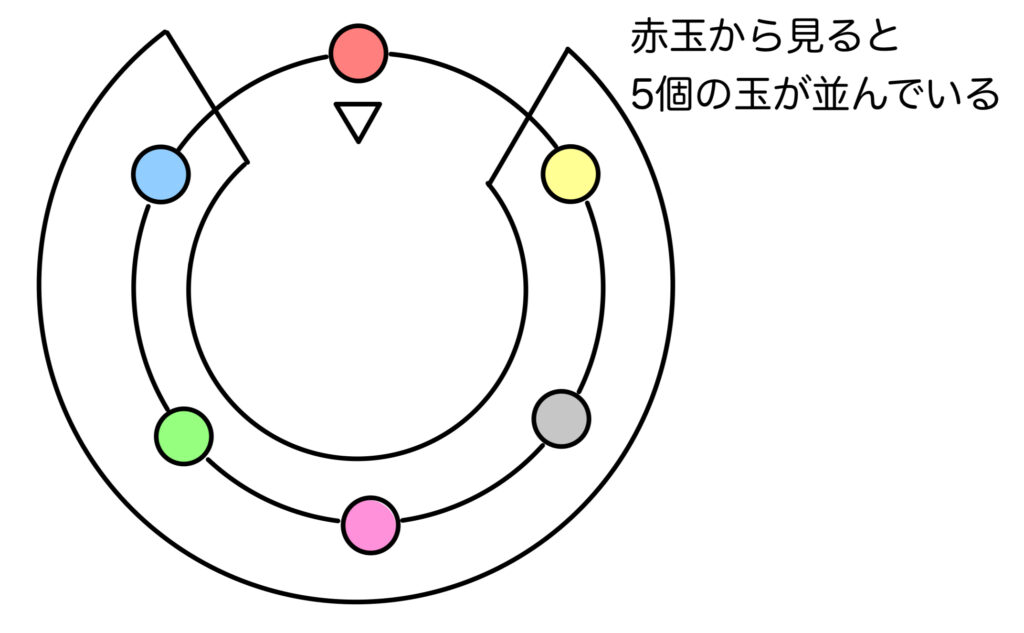
あっ。もし赤玉から見た5個の並びが違っていれば
どれだけ回転しても同じ並びにはなりませんね!
n浪君すばらしい!
つまり\((1)\) の円順列は何通りでしょう?
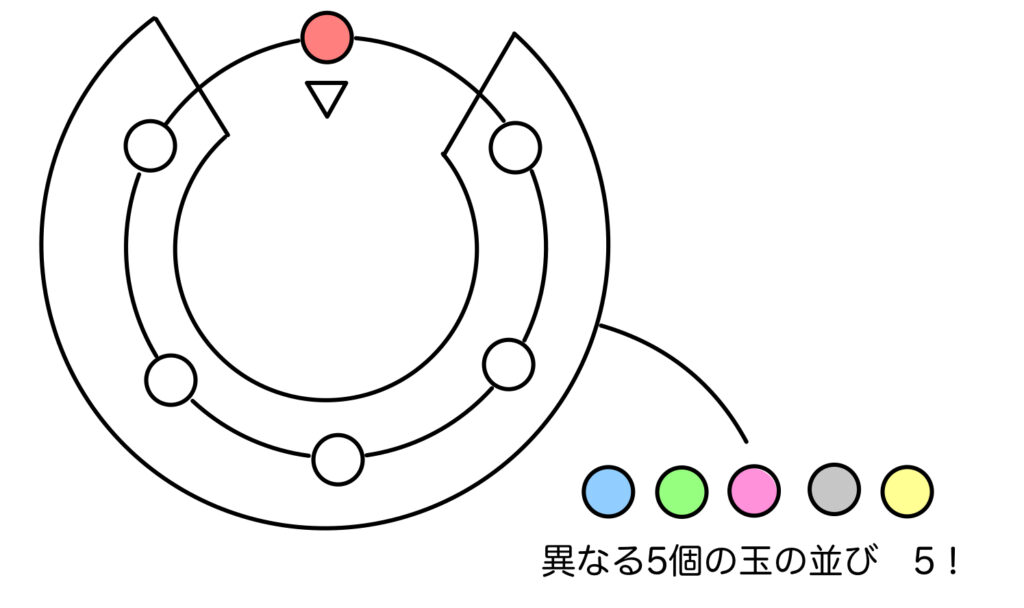
赤玉以外の異なる5個の玉の並びを考えて
\(5!=120\) 通りです。
いいですね。円順列の公式だと確かに
\((6-1)!=5!=120\) 通り
となるんですが、基準となる1個を除いた順列を計算しているんですね。
先生!じゃあ「じゅず順列」はどうなるんですか?
円順列で考えた\(120\) 通りがありますね?
これらには\(60\) 通りの線対称なペアがあります。
このペアは裏返すと同じじゅずとみなせるのです。
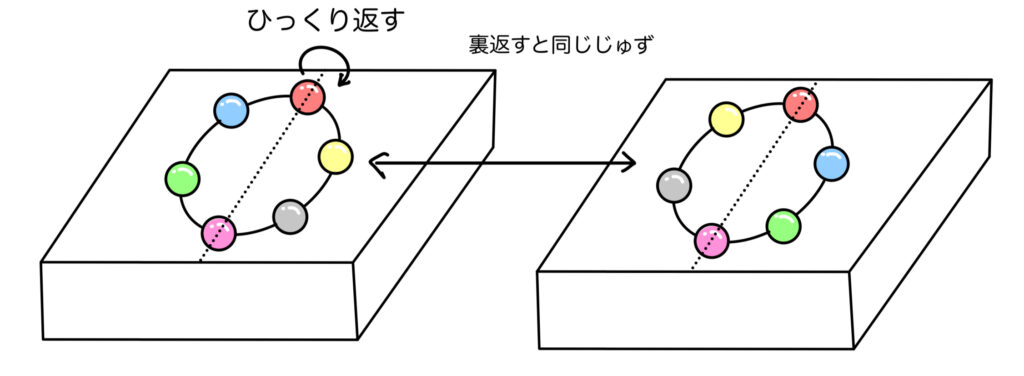
なるほど!円順列では\(2\) 通りと数えてたものが\(1\) 通りにまとまるんですね。
てことは…\(120\div{2}=60\) 通り となるのか。
OKです。
これはすべて異なる色の玉であるから\(\div{2}\)
でいいんですが、同じ色があったりするとそうはいかないんです。
だから先生は公式を覚えないようにって言ってたんですね~。
わかりました!もう少し応用的な円順列・じゅず順列の問題もやってみます!




コメント