先生!問題を解いていたら
\(_6\rm{C}_4\) とかよくわからない記号が出てきました…。
こないだ勉強した順列の記号 \(\rm{P}\) とはどう違うんですか?
これは組合せの計算で用いる記号 \(\rm{C}\) ですね。
まずは計算方法の前に問題をやってみましょう。
\(\rm{A,B,C,D,E}\) の異なる5文字がある。以下の問いに答えよ。
\((1)~~\) 3つ選んで1列に並べる方法は何通りあるか。
\((2)~~\) 3つ選んだ組み合わせの方法は何通りあるか。
\((1)\) は順列の問題ですね。
計算は\(_5\rm{P}_3=5\times4\times3=60\) 通りです!
OKです。では\((2)\) を解くついでに、
\(\rm{C}\) の記号も説明しましょう。
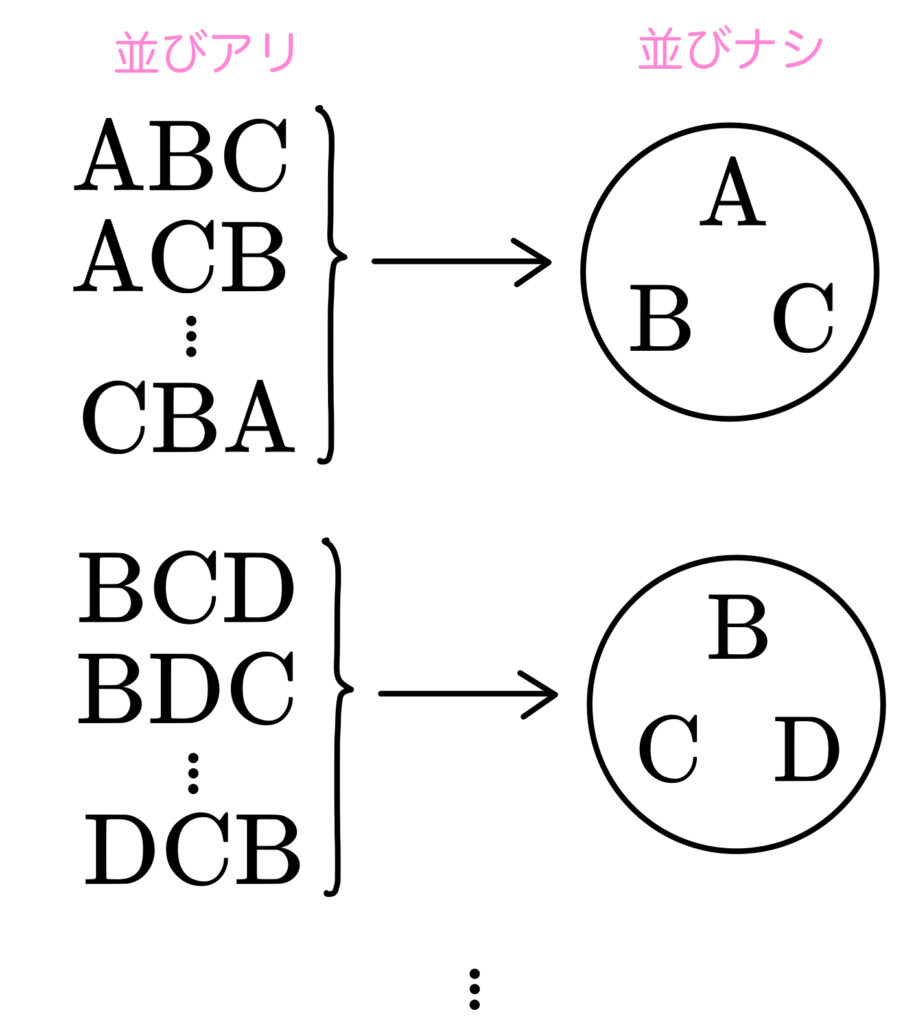
\((1)\) では3文字の並べ方まで考えていたのに対して、
\((2)\) は並びはなく文字の組のみ考えます。
じゃあ\((1)\) で求めた\(60\) 通りを
3文字の並べ方 \(3!\) で割ると組の数がでますね。
つまり\(60\div{3!}=60\div{6}=10\) 通りです。
正解です。まずは3文字並べてから、
その並び順で割れば組合せの数になりますね。
まとめると計算式は…
\(\dfrac{_5\rm{P}_3}{3!}=\dfrac{5\cdot4\cdot3}{3\cdot2\cdot1}=10\)
となりますね。
はい。
ところで組合せの記号 \(C\) はどこに出てくるんですか?
ここを\(_5\rm{C}_3\) と定めるのです。

つまり、\(_5\rm{C}_3=\dfrac{5\cdot4\cdot3}{3\cdot2\cdot1}=10\)
と計算するんですね。
それだけかぁ。
じゃあ \(_6\rm{C}_4=\dfrac{6\cdot5\cdot4\cdot3}{4\cdot3\cdot2\cdot1}=15\)
のように計算すればいいんですね。
いいですね。
計算のポイントは約分しやすいように、
分母と分子は掛け算のままにして計算するといいでしょう。
じゃあいくつか問題を解いて確認します!
\((1)~~\)6人の生徒から、3人を選ぶ方法は何通りあるか。
\((2)~~\)7個の異なる色から、2色選ぶ方法は何通りあるか。
\((1)~~_6\rm{C}_3=\dfrac{6\cdot5\cdot4}{3\cdot2\cdot1}=20\) 通り
\((2)~~_7\rm{C}_2=\dfrac{7\cdot6}{2\cdot1}=21\) 通り
これだけでいいんですね~。
では次回は、もう少し組合せの記号 \(C\) について学んでいきましょう。




コメント