先生!組合せの記号 \(\rm{C}\) の使い方はわかりました。
今日はこれを使ってこの問題を解きたいです!
9人を次のように分ける方法は何通りあるか。
\((1)~~\)4人,3人,2人の3組に分ける。
\((2)~~\)3人ずつ, 3組に分ける。
\((3)~~\)5人,2人,2人の3組に分ける。
これは組分けと呼ばれる重要な問題ですね。
ではまず\((1)\) をやってみましょう。
9人はすべて異なるという前提も忘れずに。
4人グループのメンバーの決め方は…
9人から4人選ぶ方法だから\(_9\rm{C}_4\) 通りですね。
残り5人から、さらに3人グループのメンバーを決めるから…
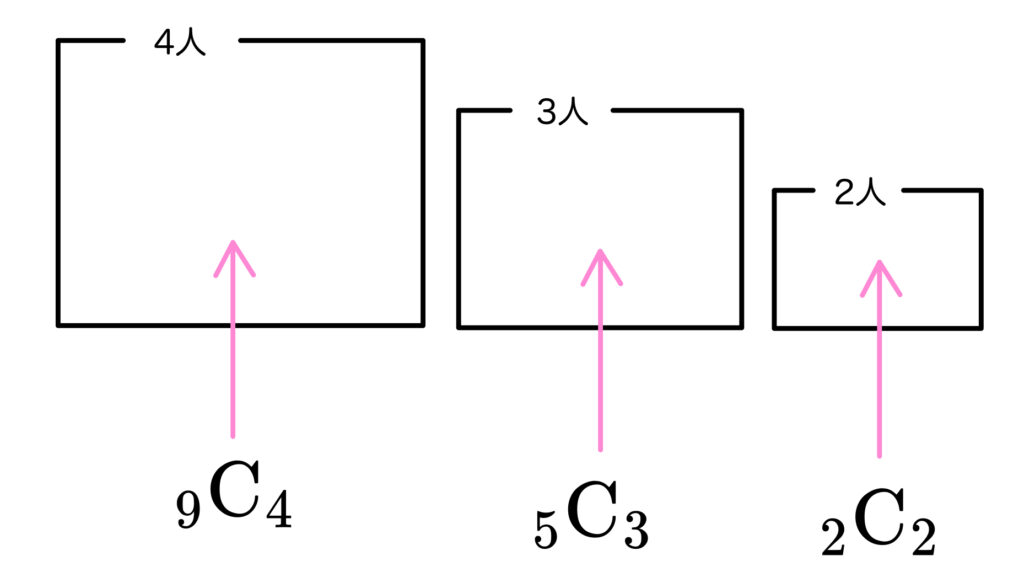
よし。4人グループのメンバーの決め方に対して,
それぞれ3人グループのメンバーの決め方,さらに
それぞれ2人グループのメンバーの決め方があるから…
積の法則で
\(~~~~_9\rm{C}_4\times{_5\rm{C}_3}\times{_2\rm{C}_2}\)
\(=126\times{10}\times{1}=1260\) 通り です。
正解です!
この考え方が基本になります。
では\((2)\) はどうでしょう?
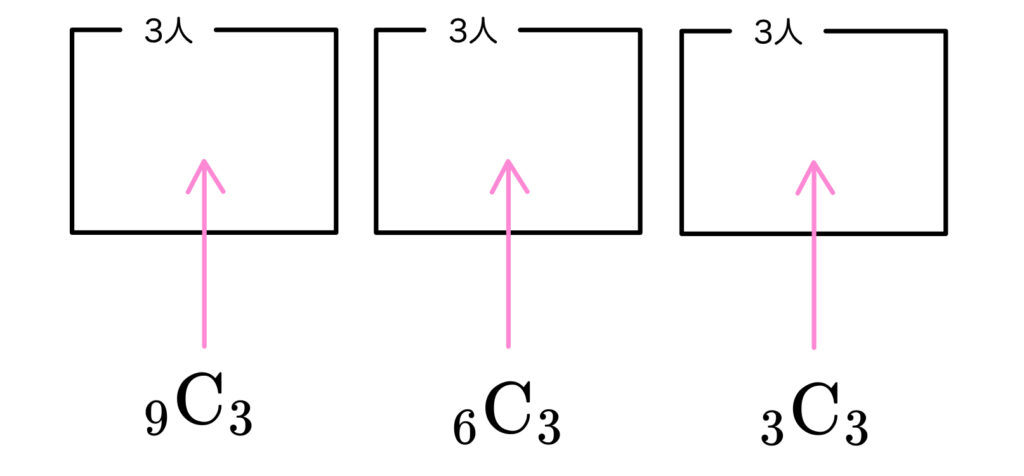
\((1)\) と同じようにやってみました~。
\(~~~~_9\rm{C}_3\times{_6\rm{C}_3}\times{_3\rm{C}_3}\)
\(=84\times{20}\times{1}=1680\) 通り です!
残念..不正解です。実は\((1)\) と同じようにはいかないんです。
これは各グループの人数がポイントです。
あっ、\((1)\) はグループの人数が全部違うのに対して,
\((2)\) は同じ人数ですね~。
まずはn浪君が求めた \(1680\) 通りが何を意味しているか
教えましょう。次を見てください。
9人にア~ケと名前をつけました。
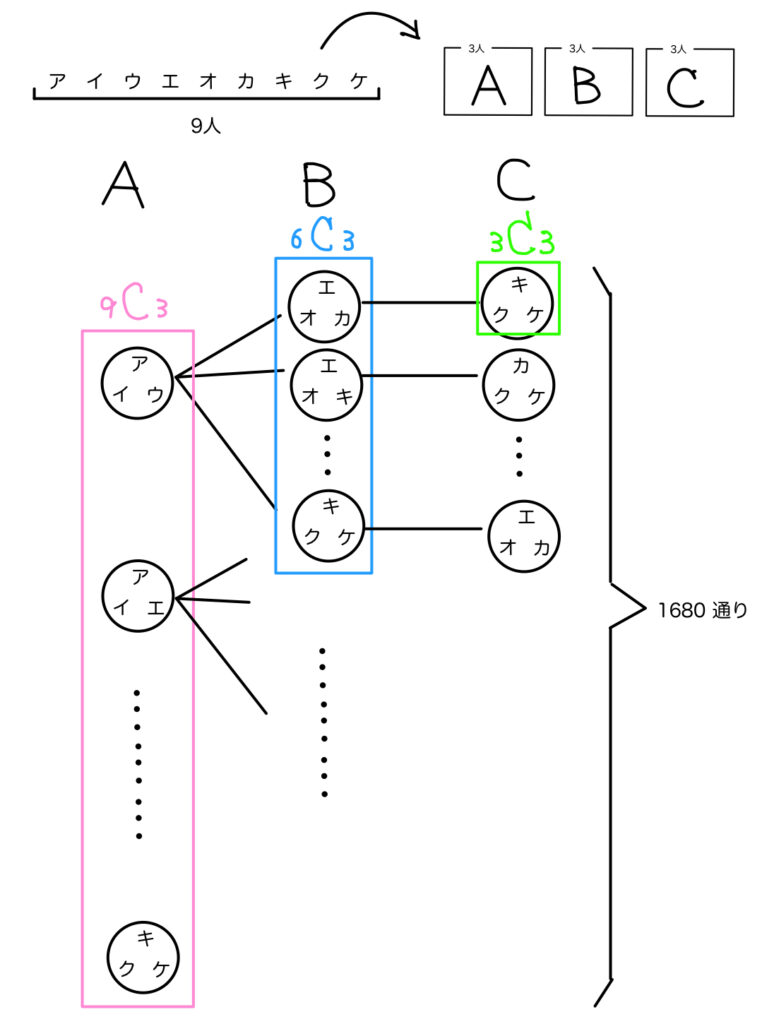
あ、僕の計算だと名前の付いたA,B,Cの3部屋に
3人ずつ分けた計算になってしまうのか~。
上の樹形図には(キ,ク,ケ)が3回登場してますもんね…。
そうなんです。
全部が異なる人数であればいいんですが、
同じ人数だと樹形図で余計に考えていることになります。
じゃあ組だけにするには、この3人が入る部屋A,B,Cの
区別を取る必要がありますね!
はい。たとえば、(ア,イ,ウ)(エ,オ,カ)(キ,ク,ケ)
は以下のような部屋分けがあります。
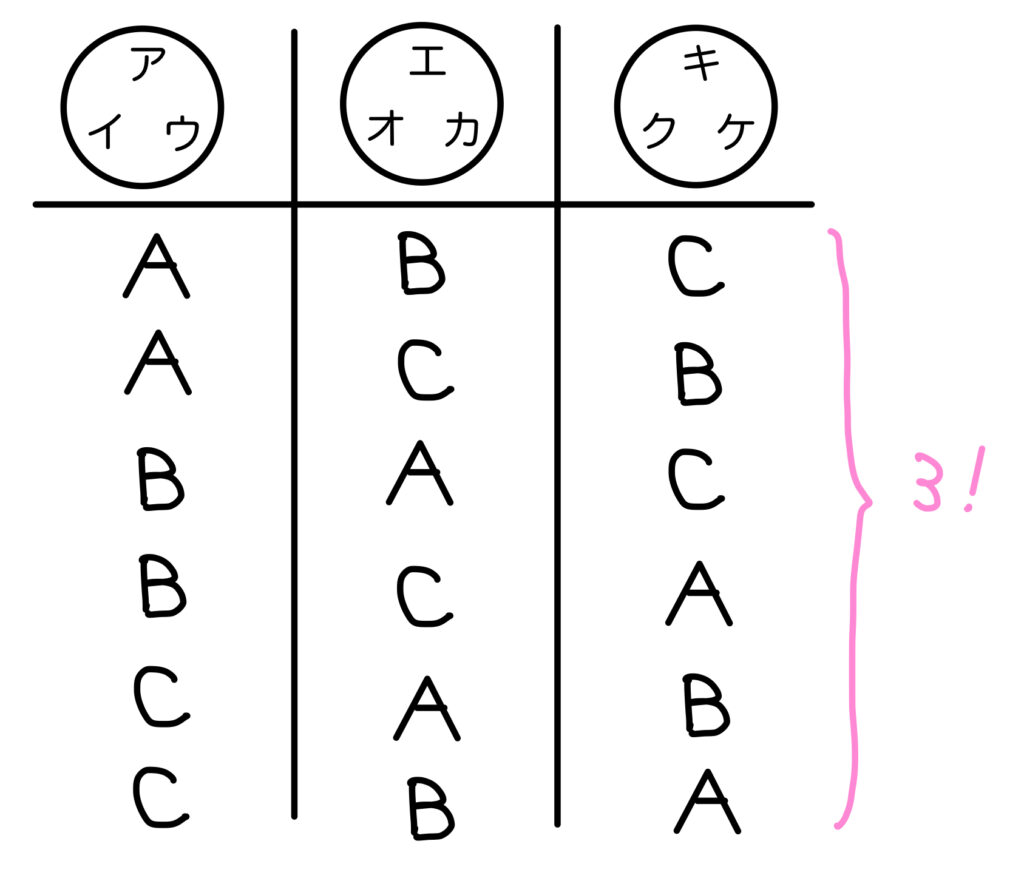
ってことは、このA,B,Cのパターン \(3!\) で
さっきの\(1680\) 通りを割ることで組分けになりますね。
つまり\(\dfrac{1680}{3!}=280\) 通りです!
正解です。では最後に\((3)\) を解いてみましょう。
自力で解いてみます!
まずは5人のグループのメンバーの決め方に対して、
2人グループのメンバーを決めて…
人数が同じ組は部屋分けの区別をとって…
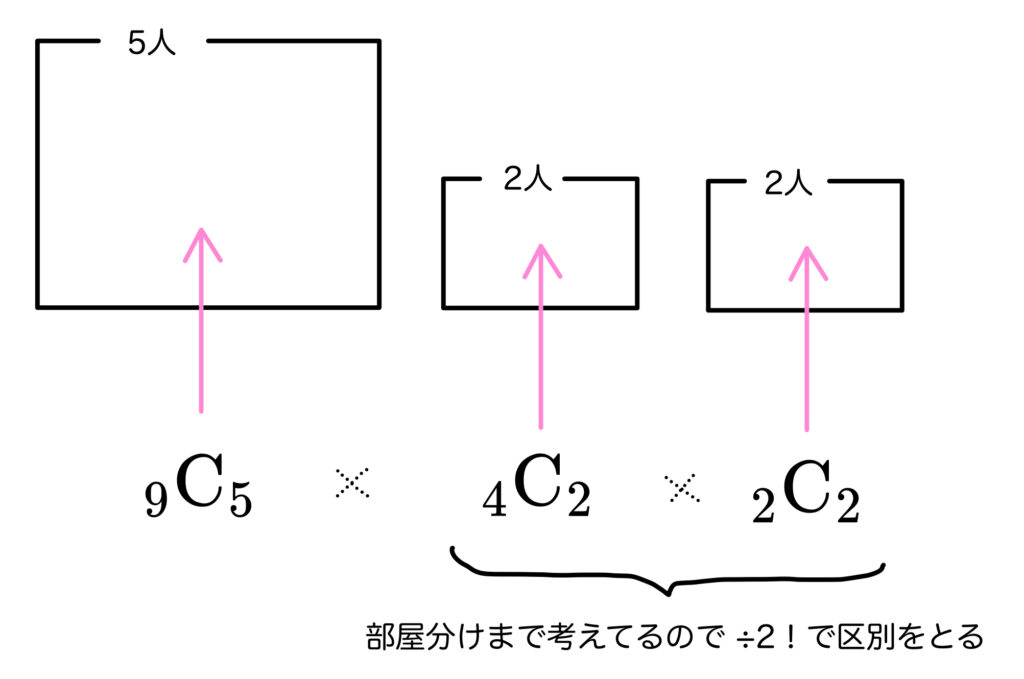
\(~~~~_9\rm{C}_5\times\dfrac{{_4\rm{C}_2}\times{_2\rm{C}_2}}{2!}\)
\(=126\times\dfrac{6\times1}{2}=378\) 通り となりました。
完璧です。これで理解できましたね。




コメント