先生!今日は三角比について教えてください。
サイン,コサイン,タンジェント,…くらいは聞いたことがありますが。
n浪君。いきなり三角比の説明に入る前に、ちょっと見てほしい図があります。
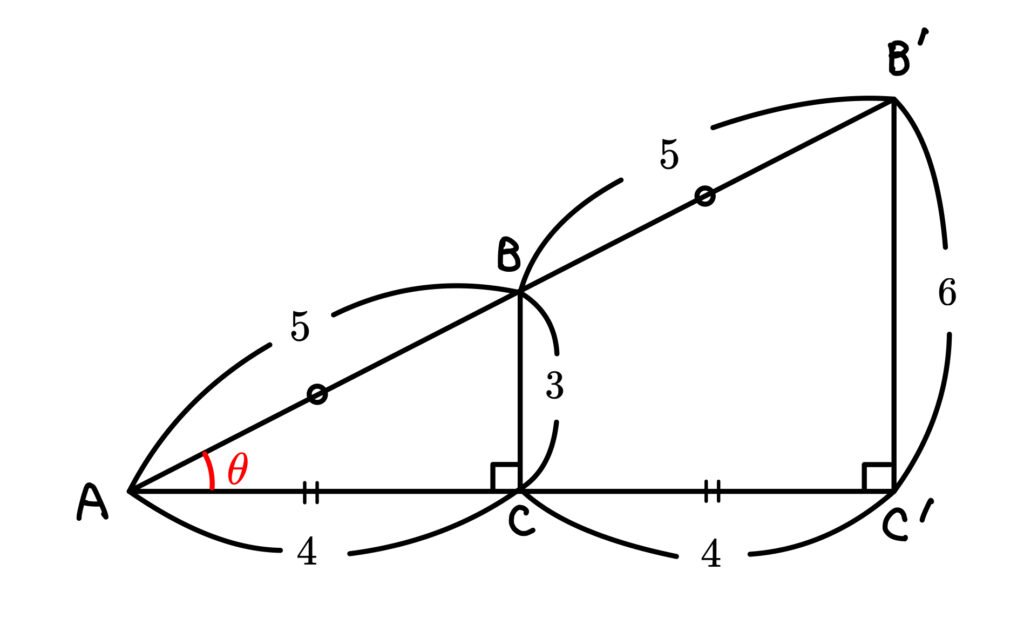
相似な直角三角形ですね~。
で、なにが始まるんですか?
n浪君にはまず, \(\triangle\rm{ABC}\) と \(\triangle\rm{AB’C’}\)
\(\frac{高さ}{斜辺}\) の値を求めてみてほしいんです。
そんな簡単なことですか?
え~と、\(\triangle\rm{ABC}\) については \(\frac{3}{5}\)
\(\triangle\rm{AB’C’}\) については \(\frac{6}{10}=\frac{3}{5}\)
どっちも同じ値ですね!
はい。結論から言うと,その値が \(\color{red}{\sin\theta}\) です。
相似な直角三角形ならこの値はいつも同じですよね。
たしかに。\(\frac{高さ}{斜辺}=\frac{3}{5}\) って
言われれば,大きさはわかんなくても形はわかりますね。
そうなんです。
\(\sin\theta\) の値だけで、直角三角形の形は1通りに決まることが重要です。
じゃあコサインとかタンジェントっていうのはなんですか?
\(\cos\theta\) や \(\tan\theta\) の値も, \(\sin\theta\) と同様
直角三角形の形を決める代表的な値です。
では定義を見てみましょう。
\(0^{\circ}<\theta<90^{\circ}\) とする。
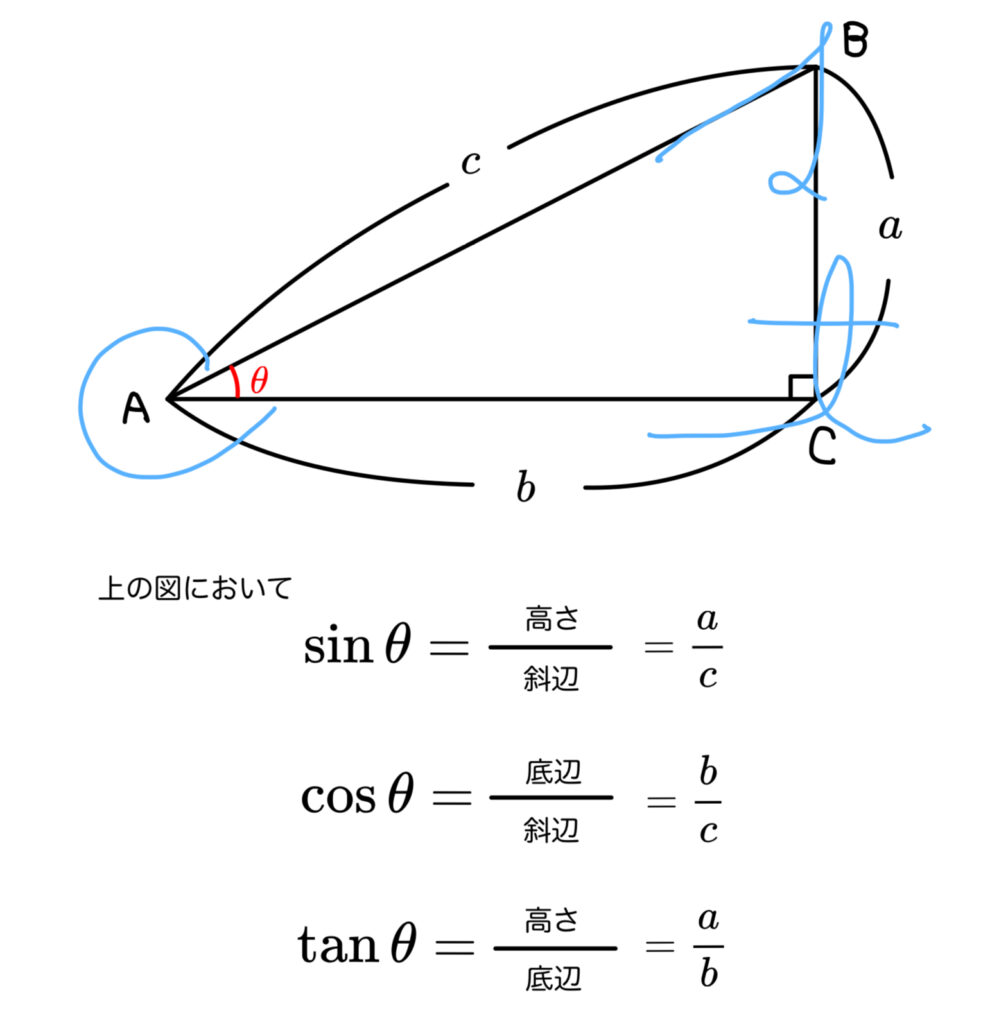
\(\sin\) を正弦,\(\cos\) を余弦,\(\tan\) を正接と言ったりします。
なるほど、代表的な3つの値がサイン,コサイン,タンジェントなんですね~。
じゃあ、さっきの図だと…。

\(\sin\theta=\frac{3}{5}\) , \(\cos\theta=\frac{4}{5}\) , \(\tan\theta=\frac{3}{4}\)
ってことか。
では、問題で確認してみましょう。
以下の図において, \(\sin\alpha~,~\cos\alpha~,~\tan\alpha\) と \(\sin\beta~,~\cos\beta~,~\tan\beta\) を求めよ。
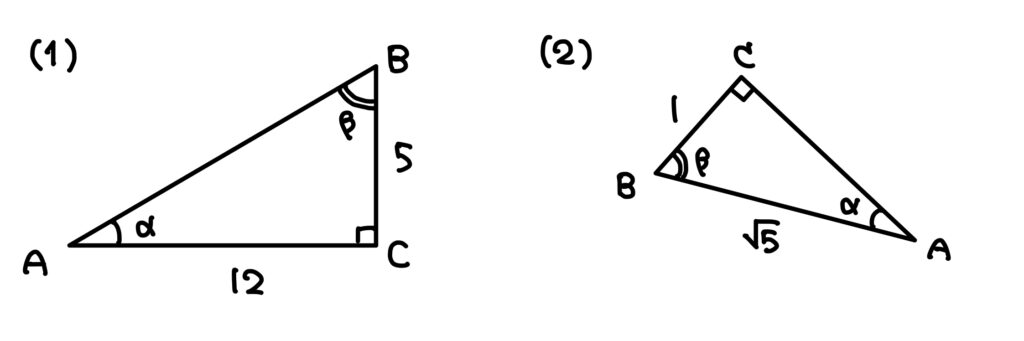
\((1)\) をやってみます!
あれ,斜辺の長さが書いてないぞ…。
でも三平方の定理で求まるか!
\(\mathrm{AB}=\sqrt{12^2+5^2}=\sqrt{169}=13\) だから…
\(\sin\alpha=\frac{5}{13}~,~\cos\alpha=\frac{12}{13}~,~\tan\alpha=\frac{5}{12}\)
ですね~。
\((1)\) の \(\beta\) については
どこを 斜辺,底辺,高さ とみるべきか注意してください。
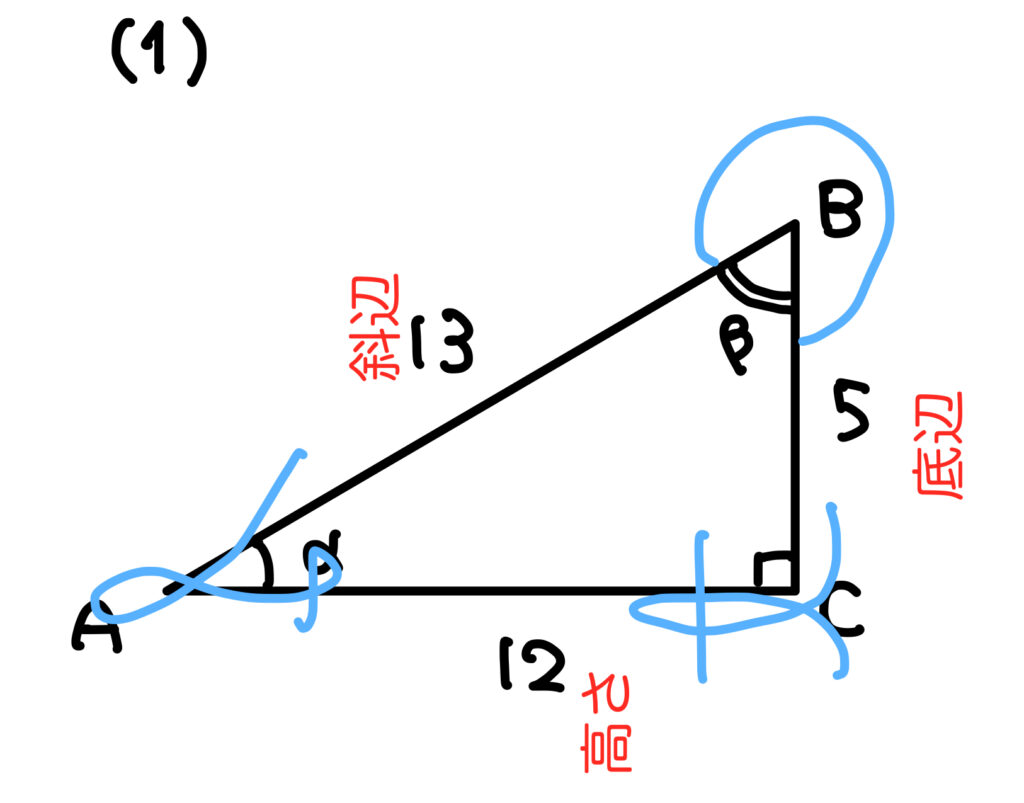
そっか。角に対して見方を変えなきゃいけませんね。
すると,\(\sin\beta=\frac{12}{13}~,~\cos\beta=\frac{5}{13}~,~\tan\beta=\frac{12}{5}\)
で合ってますか?
正解です!
では \((2)\) は自力でできますか?
まずは三平方の定理で残りの辺の長さを求めて…
\(\mathrm{AC}=\sqrt{\sqrt{5}^2-1}=\sqrt{4}=2\)
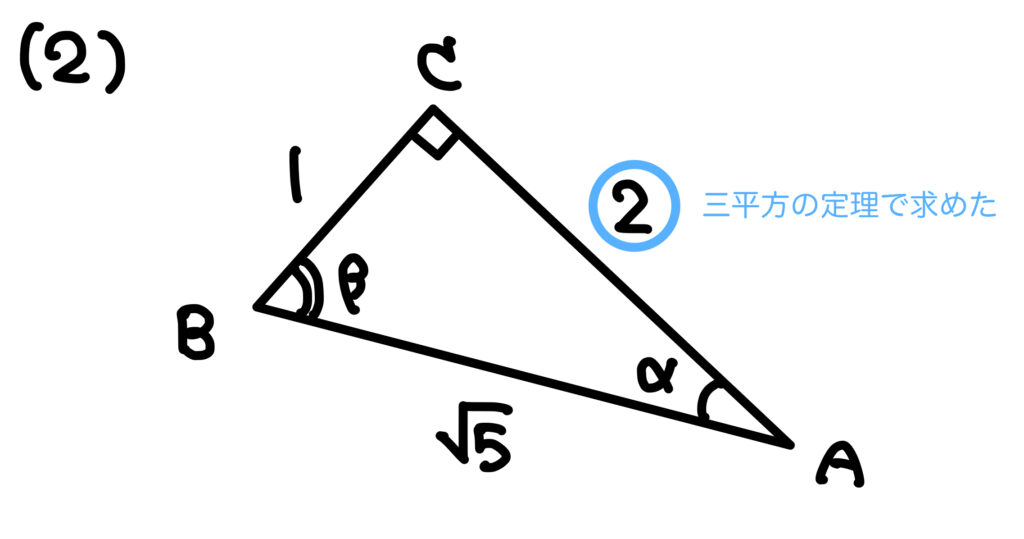
さぁ後はそれぞれの角について見方に注意していきましょう。
\(\sin\alpha=\frac{1}{\sqrt{5}}~,~\cos\alpha=\frac{2}{\sqrt{5}}~,~\tan\alpha=\frac{1}{2}\)
\(\sin\beta=\frac{2}{\sqrt{5}}~,~\cos\beta=\frac{1}{\sqrt{5}}~,~\tan\beta=\frac{2}{1}=2\)
よし!全部求められました!
大正解です。それでは次回は有名角の三角比について学びましょう。




コメント