\(2x^2-5xy-3y^2+7x+7y-4\) を因数分解せよ。
2文字以上の文字があり,共通因数が見えないので「次数の低い文字」について整理する。
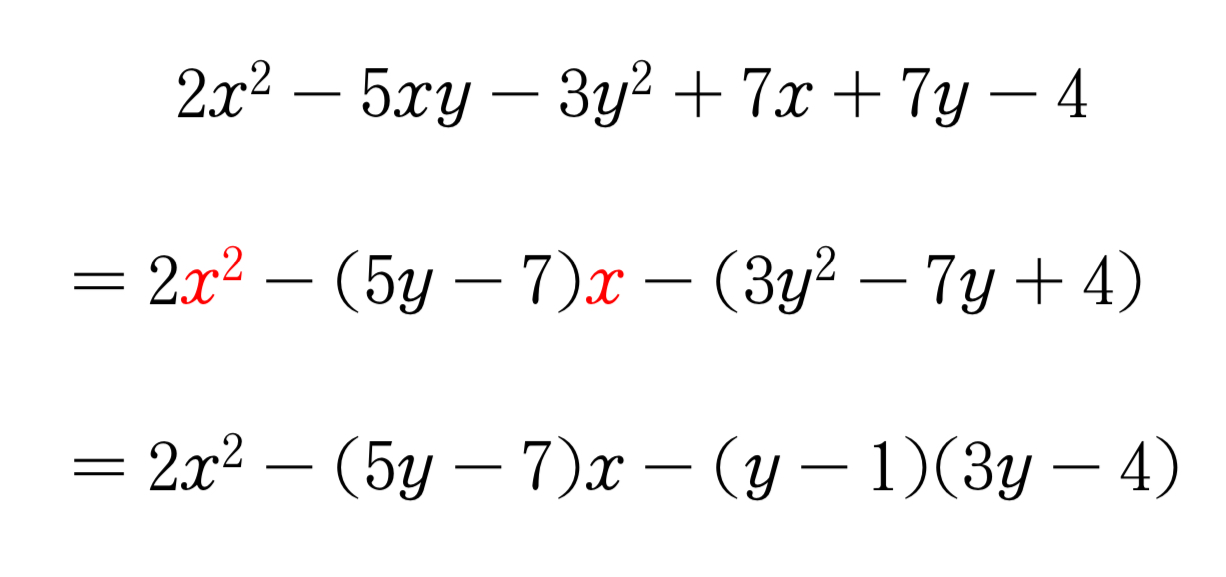
あとは \(x\) の2次式なので「たすきがけ」ですね。
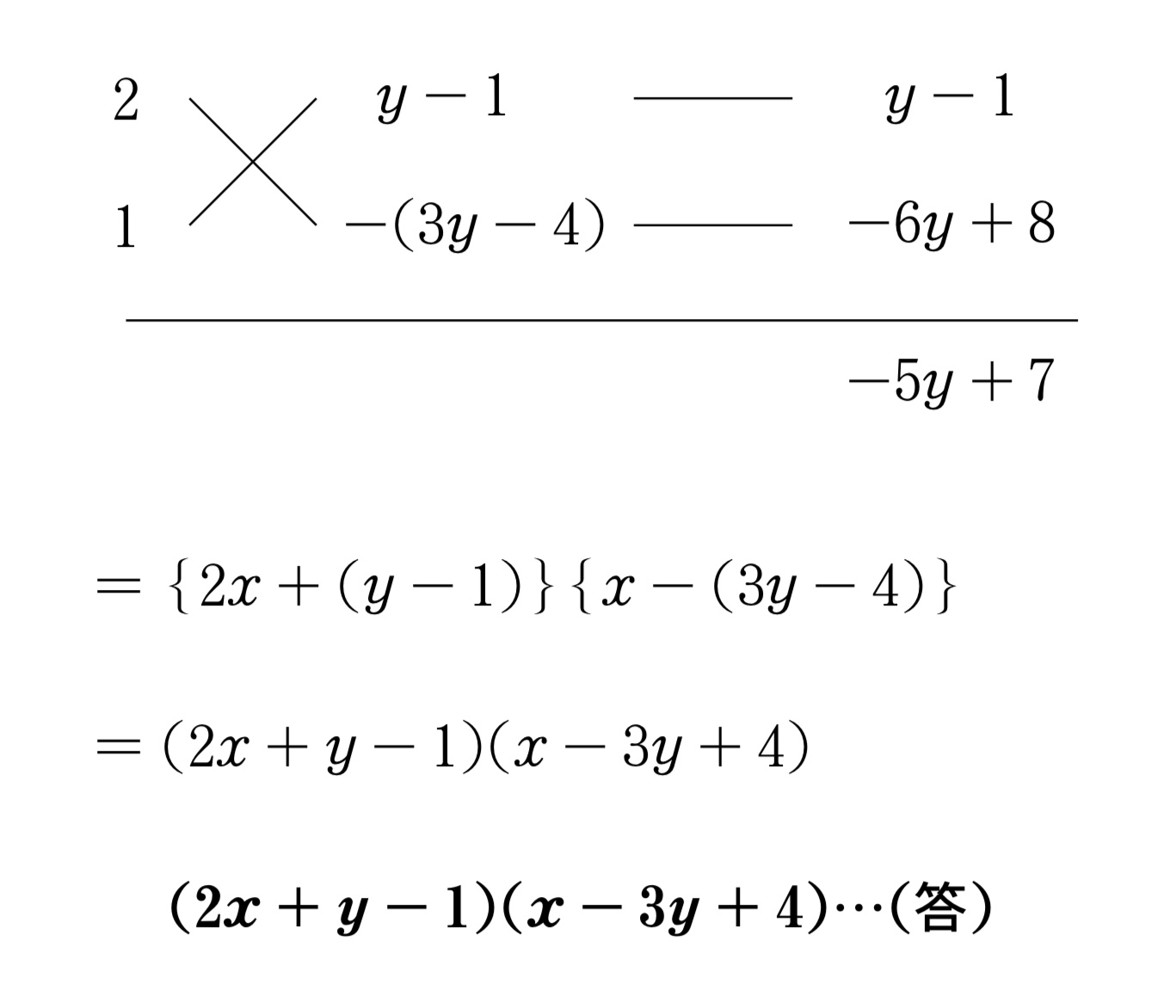
$2x^2-5xy-3y^2+7x+7y-4$\ $=2\textcolor{red}{x^2}-(5y-7)\textcolor{red}{x}-(3y^2-7y+4)$\ $=2x^2-(5y-7)x-(y-1)(3y-4)$\\ \begin{tikzpicture}[scale=0.2, baseline=5.0pt] \coordinate (O) at (0,4) node [] at (O){2}; \coordinate (O) at (0,0) node [] at (O){1}; \coordinate (O) at (10,4) node [] at (O){$y-1$}; \coordinate (O) at (11,0) node [] at (O){$-(3y-4)$}; \drawfill=white,rounded corners=1pt — (6,4); \drawfill=white,rounded corners=1pt — (6,0); \drawfill=white,rounded corners=1pt — (21,0); \drawfill=white,rounded corners=1pt — (21,4); \coordinate (O) at (26,4) node [] at (O){$y-1$}; \coordinate (O) at (26,0) node [] at (O){$-6y+8$}; \drawfill=white,rounded corners=1pt — (30,-3); \coordinate (O) at (26,-5) node [] at (O){$-5y+7$}; \end{tikzpicture}\\ $=\B{2x+(y-1)}\B{x-(3y-4)}$\ $=(2x+y-1)(x-3y+4)$\ ~~$\bd{(2x+y-1)(x-3y+4)\cdots(答)}$




コメント