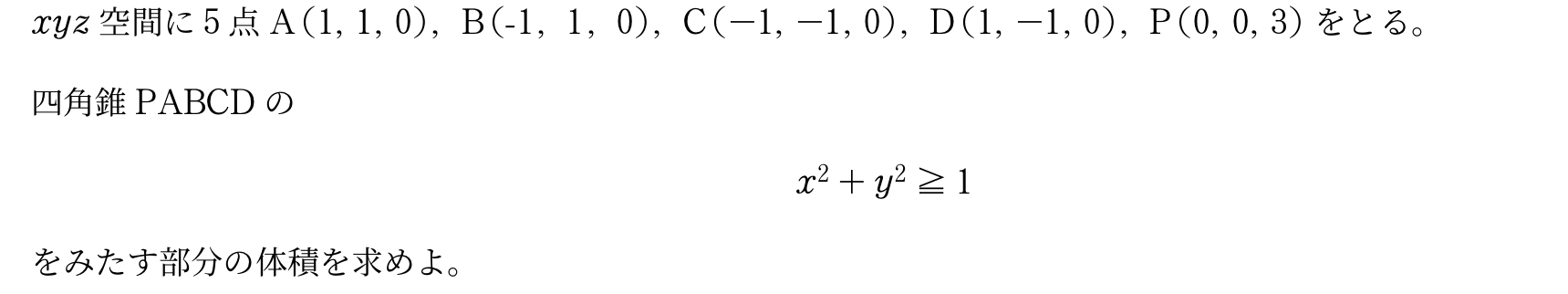
立体のイメージがわかないので,とりあえず平面 \(z=t\) 上でどんな断面なのかを考察してみよう。
断面は正方形の内部と円の外部の共通部分であることがわかった。
断面が存在する条件に注意して,断面積を求めよう。
このとき扇形の面積を記述するために置き換えをする。

あとはθで積分して終了。

$xyz$空間に5点A\,($1,1,0$),B\,(-1,1,0),C\,($-1,-1,0$),D\,($1,-1,0$),P\,($0,0,3$)をとる。
四角錐PABCDの
$x^2+y^2\geqq{1}$
をみたす部分の体積を求めよ。
体積を求める部分の立体を$K$と名づける。
平面$z=t~(0\leqq{t}\leqq{3})$ による$K$の断面積は1辺$1-\bunsuu{t}3$の正方形の内部と,
円$x^2+y^2\geqq{1}$ の共通部分の面積である。
\includegraphics[scale=0.6]{toudaie2.ai}
共通部分が存在する条件は,$1\leqq\sqrt{2}\p{1-\bunsuu{t}3}$,すなわち$0\leqq{t}\leqq{3}\p{1-\bunsuu1{\sqrt{3}}}$である。
ここで上記の共通部分の面積を$S(t)$とおくと,$S(t)$は$x,y$についてともに対称であるから
右下図の影付きの部分の面積を4倍することによって求めよう。
$\cos\theta=1-\bunsuu{t}3$と変数を置き換えると,
\begin{tabular}{c||c}
$t$&$0\to{3}\p{1-\bunsuu1{\sqrt{3}}}$\
\hline
$\theta$&$0\to\bunsuu\pi4$\
\end{tabular}である。\
$\bunsuu14S(t)=\cos^2\theta-2\cdot\bunsuu12\sin\theta\cos\theta-\bunsuu12\p{\bunsuu\pi2-2\theta}$\
\hspace{12mm}$=\bunsuu12(1+\cos{2\theta})-\bunsuu12\sin{2\theta}+\theta-\bunsuu\pi4$\
$\yueni~S(t)=2\cos\theta-2\sin2\theta+4\theta+2-\pi$\
以上から求める体積は\
$4\dint{0}{{3}\left(1-\frac1{\sqrt{3}}\right)}S(t)\,dt=4\dint{0}{\frac{\pi}4}\p{2\cos\theta-2\sin2\theta+4\theta+2-\pi}\cdot3\sin\theta\,d\theta$\
\hspace{31mm}$=4(1+\sqrt{2})-3\pi\kotae$




コメント