
今回の主役は円錐です。空間における円錐面の方程式は書けるようにしておくとよいでしょう。
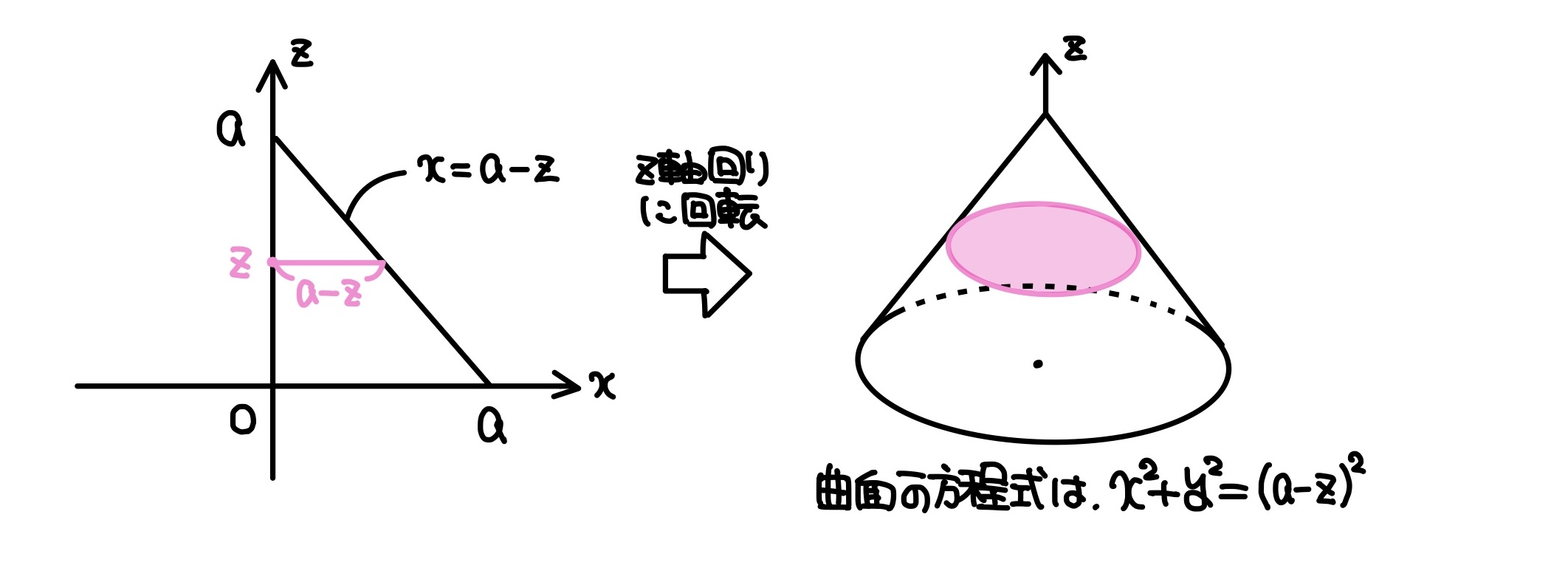
円錐面を平面 \(z=y\) で切った断面に「放物線」が現れる。
ゆえに断面は放物線で囲まれた部分を積分すればOKですね。
さて、平面Pによって分けられた2つの立体のうち,小さい方とは円錐の頂点を含まない側であることが直観的にわかります。直円錐の2等分から,この立体を除いた立体をKと名づけて積分しましょう。
じつは立体Kは底面を(1)でもとめた放物線を底面とする「錐体」です。なので錐体の体積
\(\dfrac{1}{3}\times\dfrac{2\sqrt{2}}{3}a^2\times\dfrac{1}{\sqrt{2}}a=\dfrac{2}{9}a^3\) と求めることも可能ですね。
中心O,半径$a$の円を底面とし,高さが$a$の直円錐がある。点Oを通り,底面と$45\ddo$の角度で交わる平面をPとする。
(1)この円錐をPで切るとき,その切り口の面積を求めよ。
(2)Pはこの円錐を2つの部分に分けるが,そのうちの小さい方の体積を求めよ。
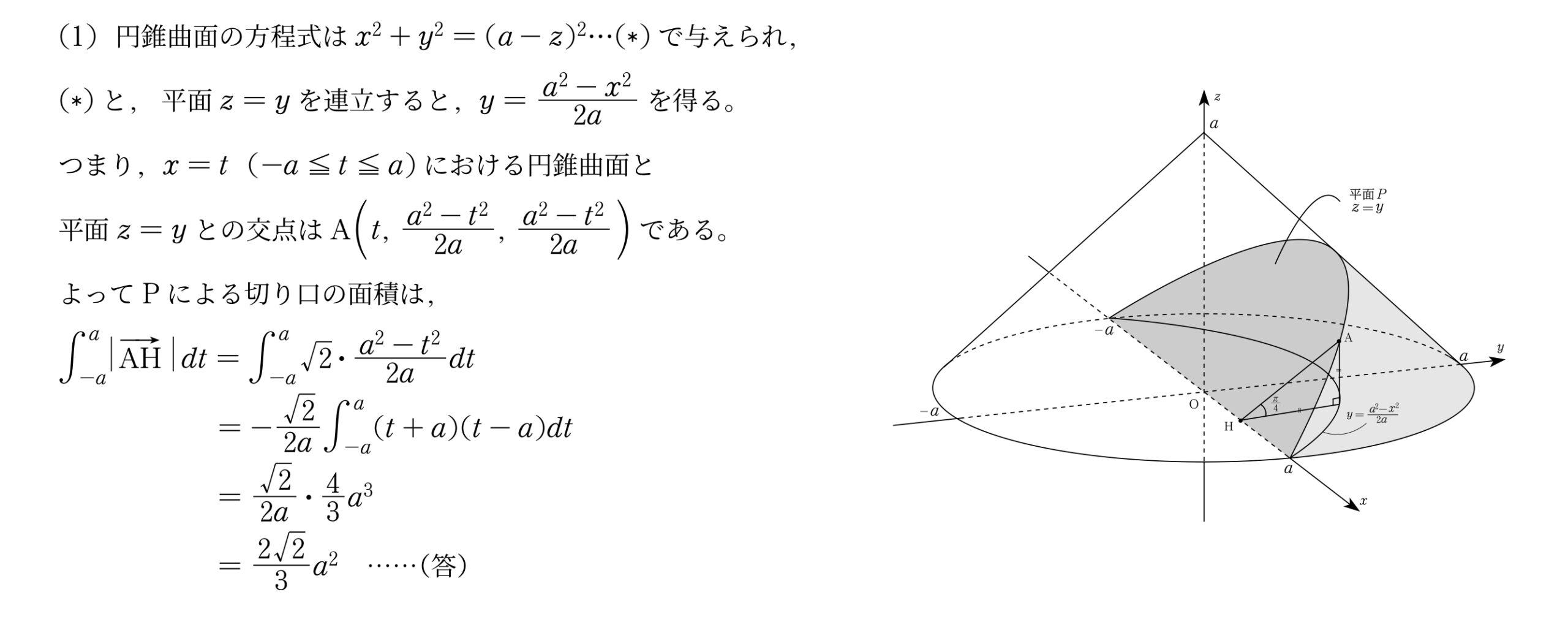
(1)円錐曲面の方程式は$x^2+y^2=(a-z)^2\cdots(\ast)$で与えられ,\ $(\ast)$と,平面$z=y$を連立すると,$y=\bunsuu{a^2-x^2}{2a}$を得る。\ つまり,$x=t(-a\leqq{t}\leqq{a})$における円錐曲面と\
平面$z=y$との交点はA$\p{t,\bunsuu{a^2-t^2}{2a},\bunsuu{a^2-t^2}{2a}}$である。\
よってPによる切り口の面積は,\
$\dint{-a}{a}\zettaiti{\Vec{AH}\,}\,dt=\dint{-a}{a}\sqrt{2}\cdot\bunsuu{a^2-t^2}{2a}dt\
=\bunsuu{\sqrt{2}}{2a}\cdot\bunsuu{4}{3}a^3\\=\bunsuu{2\sqrt{2}}{3}a^2\kotae$\\
\ymawarikomi{3}{4}{8.5cm}{waseda2004a.ai}{7cm}{32}%
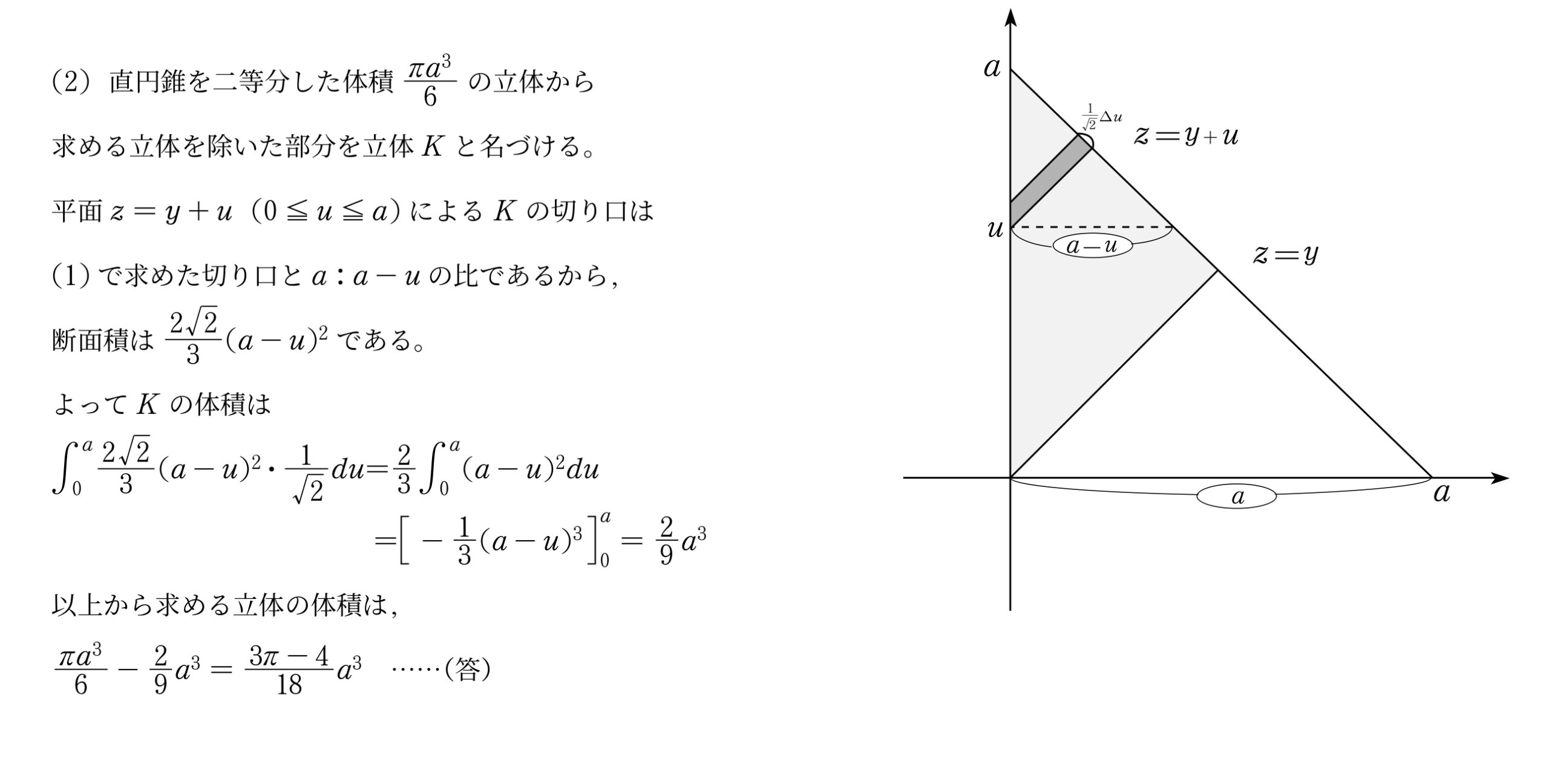
(2)直円錐を二等分した体積$\bunsuu{{\pi}a^3}{6}$の立体から 求める立体を除いた部分を立体$K$と名づける。
平面$z=y+u(0\leqq{u}\leqq{a})$による$K$の切り口は
(1)で求めた切り口と$a:a-u$の比であるから,
断面積は$\bunsuu{2\sqrt{2}}{3}(a-u)^2$である。
よって$K$の体積は
$\dint{0}{a}\bunsuu{2\sqrt{2}}{3}(a-u)^2\cdot\bunsuu1{\sqrt{2}}du$=$\bunsuu23\dint{0}{a}(a-u)^2du$
\hspace{42mm}=$\teisekibun{-\bunsuu13(a-u)^3}{0}{a}=\bunsuu29a^3$
以上から求める立体の体積は,
$\bunsuu{{\pi}a^3}{6}-\bunsuu29a^3=\bunsuu{3\pi-4}{18}a^3\kotae$




コメント