
非回転体の体積を求めるにあたって,まず重要なのは「どの平面で切るか」です。
なるべく断面が簡単に求まるほうがいいですね。例として3パターン挙げておきましょう。
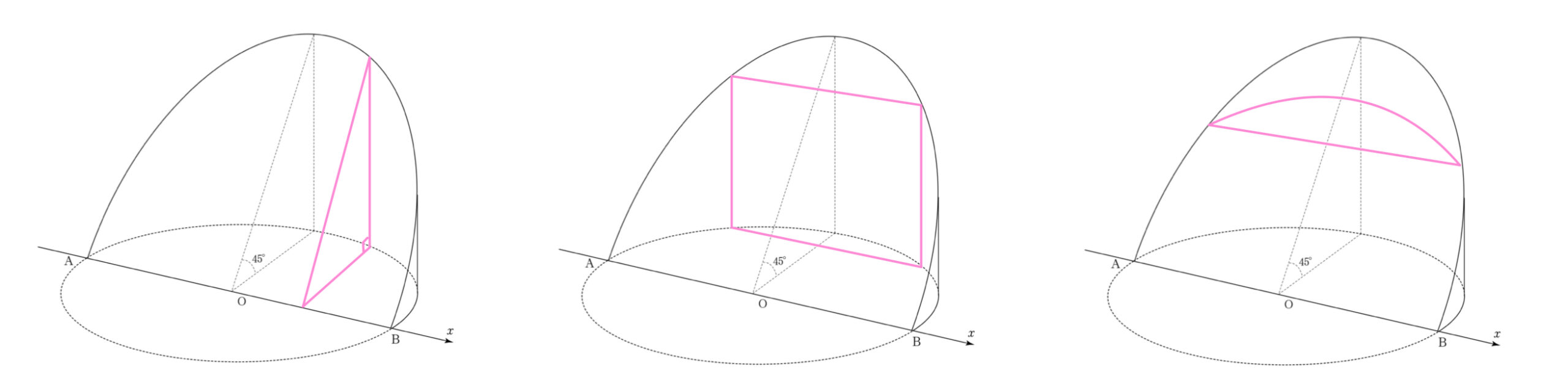
まずは断面が「直角二等辺三角形」となる左のパターンでやってみようと思います。
練習のためにも他のパターンでやってみるといいでしょう。
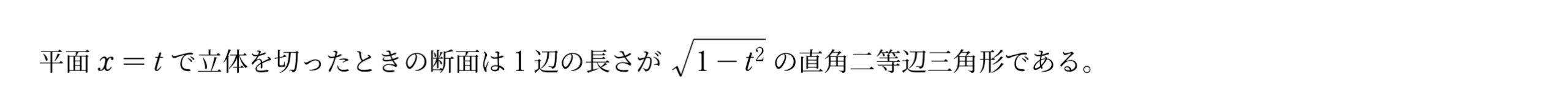
あとは断面積を求めて,ー1から1まで積分して終了です。

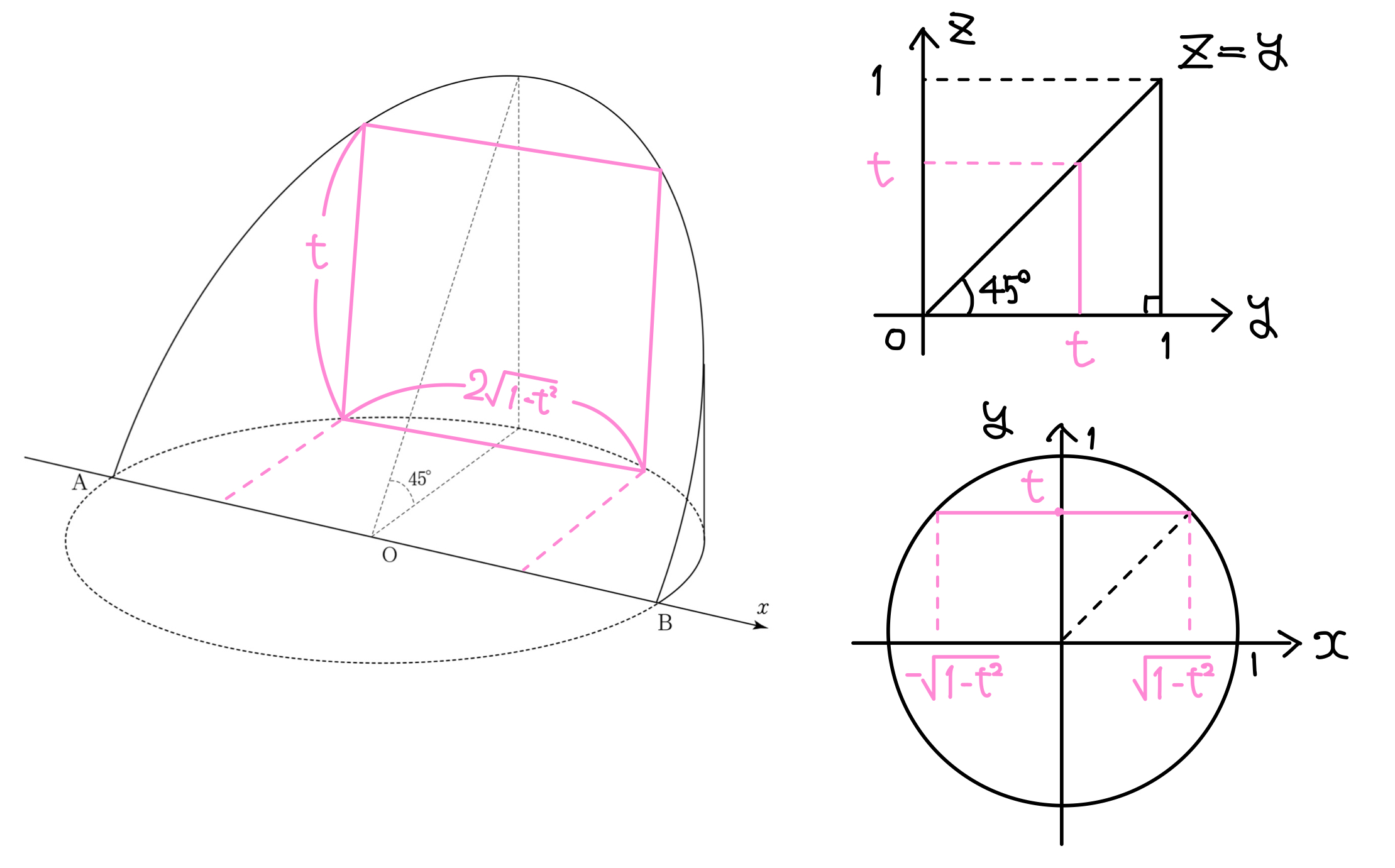
体積は求まりましたが,次に \(y\) 軸に垂直に切って求めてみましょう。

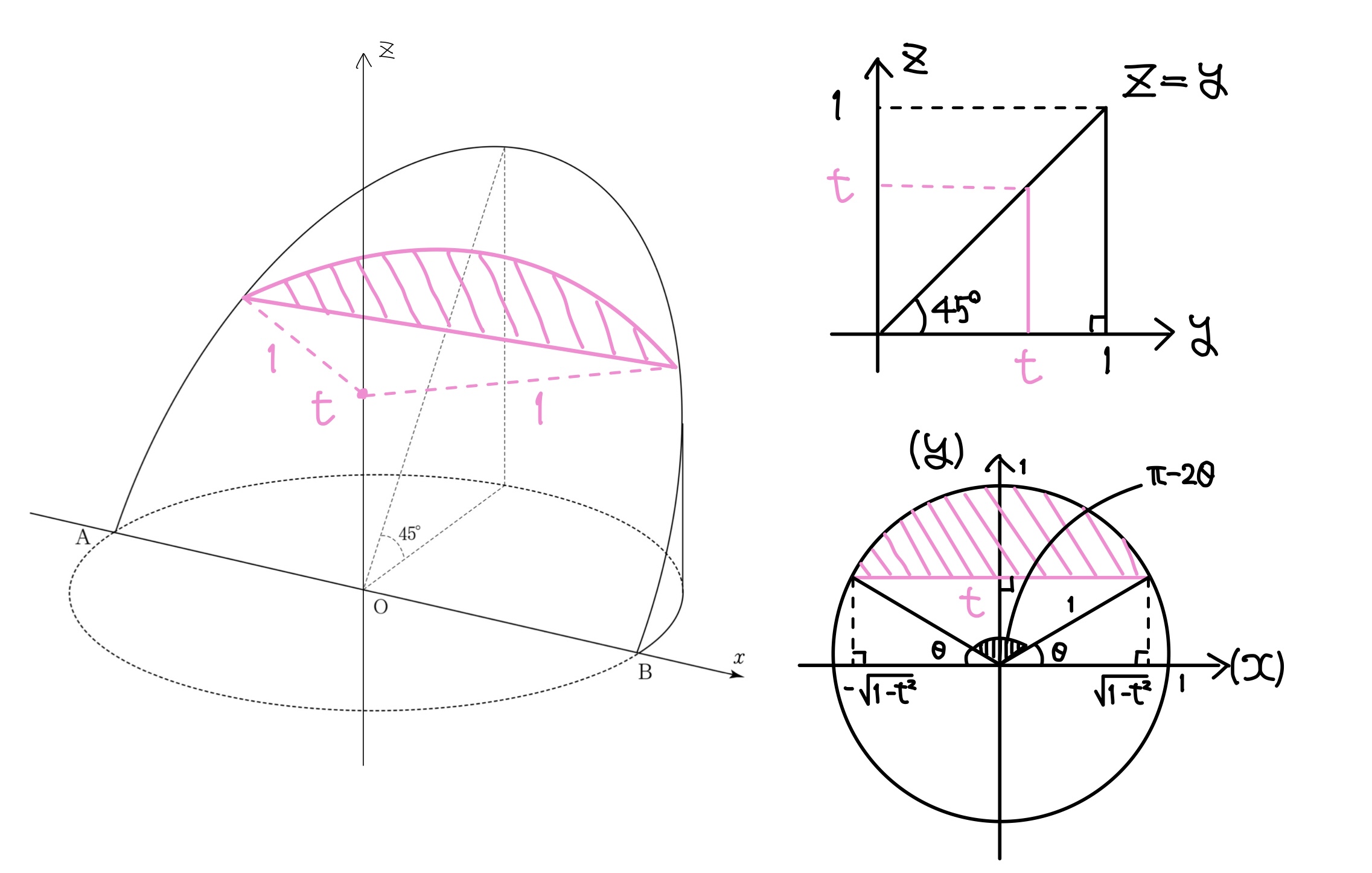
最後に \(z\) 軸に垂直に切って求めてみましょう。断面は円の一部ですので,扇形が登場します。
そのため \(t=\sin\theta\) の置き換えをしましょう。

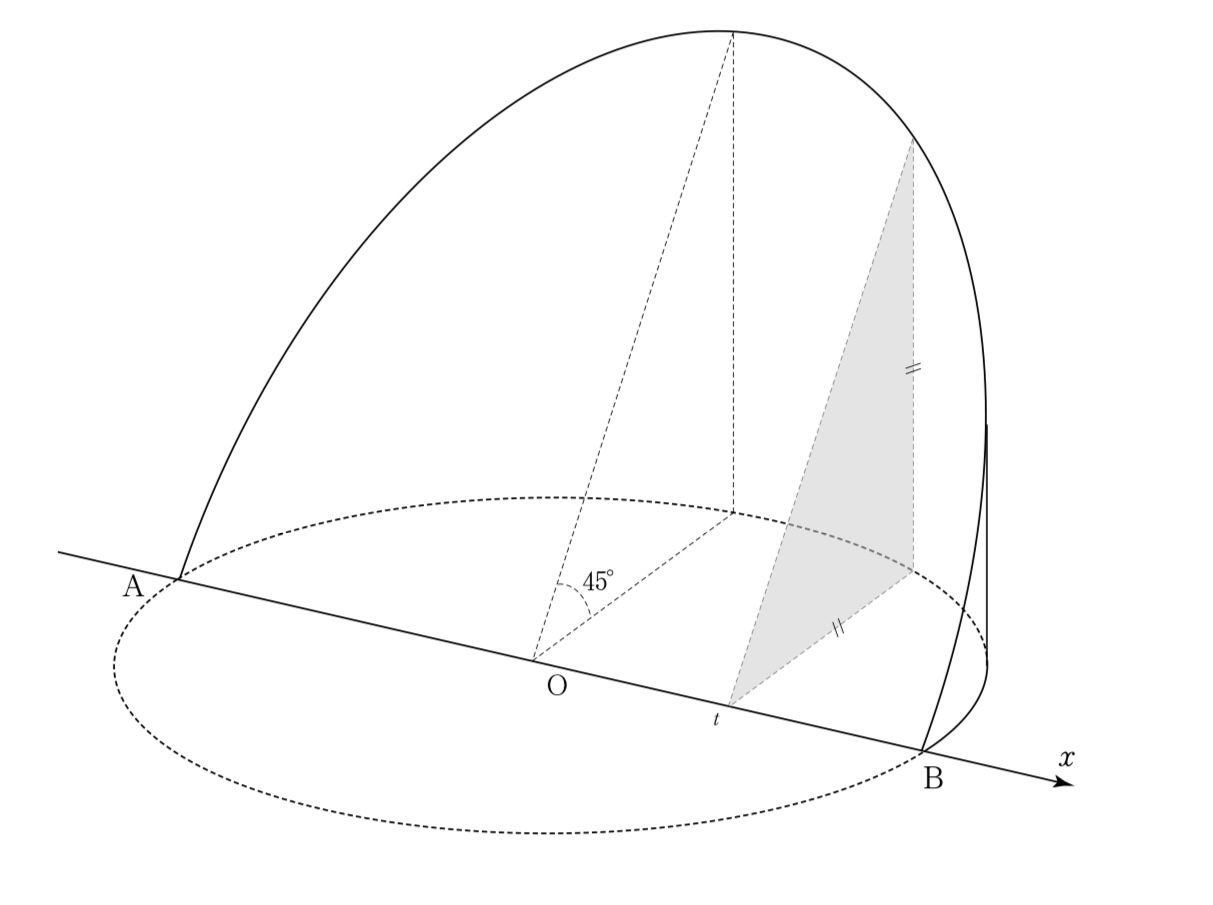
右図のように底円の半径1,高さ1の直円柱がある.底円の直径ABを通り交角$45\ddo$で底円と交わる平面でこの直円柱を切るとき,平面の下側の部分の体積を求めよ.
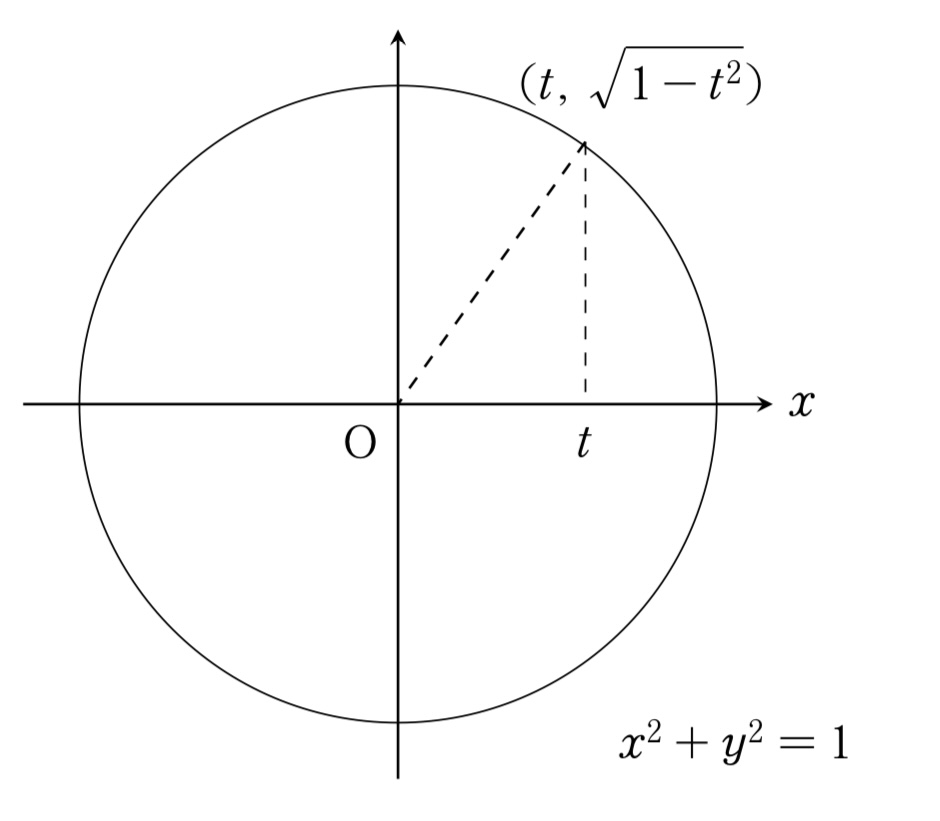
平面$x=t$で立体を切ったときの断面は1辺の長さが$\sqrt{1-t^2}$の直角二等辺三角形である。
断面積を$S(t)$とおくと,$S(t)=\bunsuu12\cdot\p{\sqrt{1-t^2}}^2=\bunsuu12(1-t^2)$\
以上から,求める立体の体積を$V$とすると,\
$V\,=\dint{-1}{1}\bunsuu12(1-t^2)\,dt\=\dint{0}{1}(1-t^2)\,dt$\ $=2\teisekibun{t-\bunsuu13t^3}{0}{1}=\bd{\bunsuu23\kotae}$
平面$y=t$で立体を切ったときの断面は,底辺$2\sqrt{1-t^2}$,高さ$t$の長方形である。\
断面積を$S_1(t)$とおくと,$S_1(t)=2t\sqrt{1-t^2}$\
以上から,\
$V=\dint{0}{1}2t\sqrt{1-t^2}\,dt$\
$=-\dint{0}{1}\sqrt{1-t^2}\cdot(-2t)\,dt$\
$=\teisekibun{-\bunsuu23(1-t^2)^{\frac32}}{0}{1}=\bd{\bunsuu23}\kotae$\
平面$z=t$で立体を切ったときの断面は,$t=\sin\theta~(\sqrt{1-t^2}=\cos\theta)$とおくと,\
~~半径1,中心角$\pi-2\theta$の扇形から,底辺$\cos\theta$,高さ$\sin\theta$の直角三角形を2つ除いた図形である。\
断面積を$S_2(t)$とおくと,$S_2(t)=\bunsuu12(\pi-2\theta)-2\cdot\bunsuu12\sin\theta\cos\theta=\bunsuu\pi2-\theta-\sin\theta\cos\theta$\
以上から,\
$V=\dint{0}{1}S_2(t)\,dt$\
$=\dint{0}{\frac\pi2}\left(\bunsuu\pi2-\theta-\sin\theta\cos\theta\right)\,\cos\theta\,d\theta$\
$=\dint{0}{\frac\pi2}\p{\bunsuu\pi2-\theta}\cos\theta\,d\theta+\dint{0}{\frac\pi2}\cos^2\theta\cdot(-\sin\theta)\,d\theta$\
$=\teisekibun{\p{\bunsuu\pi2-\theta}\sin\theta-\cos\theta}{0}{\frac\pi2}$+$\teisekibun{\bunsuu13\cos^3\theta}{0}{\frac\pi2}$\
$=1-\bunsuu13=\bd{\bunsuu23}\kotae$




コメント