先生。今日は集合と要素の個数について教えてください!
わかりました。
n浪君。まずは「集合」の記号については数Ⅰで学びましたね?
はい!そのうえでこの問題について教えてください。
\(15\) 以下の自然数全体の集合を全体集合\(U\) とする。
\(U\) の部分集合
\(A=\{1,2,4,7,8,9,12,15\}~,\)
\(B\{1,4,6,7,9\}~\)
について、次の個数を求めよ。
\((1)~~n(A)~~~~~~~~~~~~~~(2)~~n(B)~~~~~~~~~~~~~(3)~~n(A \cap{B})\)
\((4)~~n(A \cup{B})~~~~~~~~~~~~(5)~~n(\overline{A})~~~~~~~~~~~~~~(6)~~n(\overline{B})\)
\((7)~~n(\overline{A \cup{B}})~~~~~~~(8)~~n(A \cap\overline{B})~~~~~~~(9)~~n(\overline{A}\cap{B})\)
ではn浪君。まずはベン図に書いてみましょう
とりあえず書いてみました。
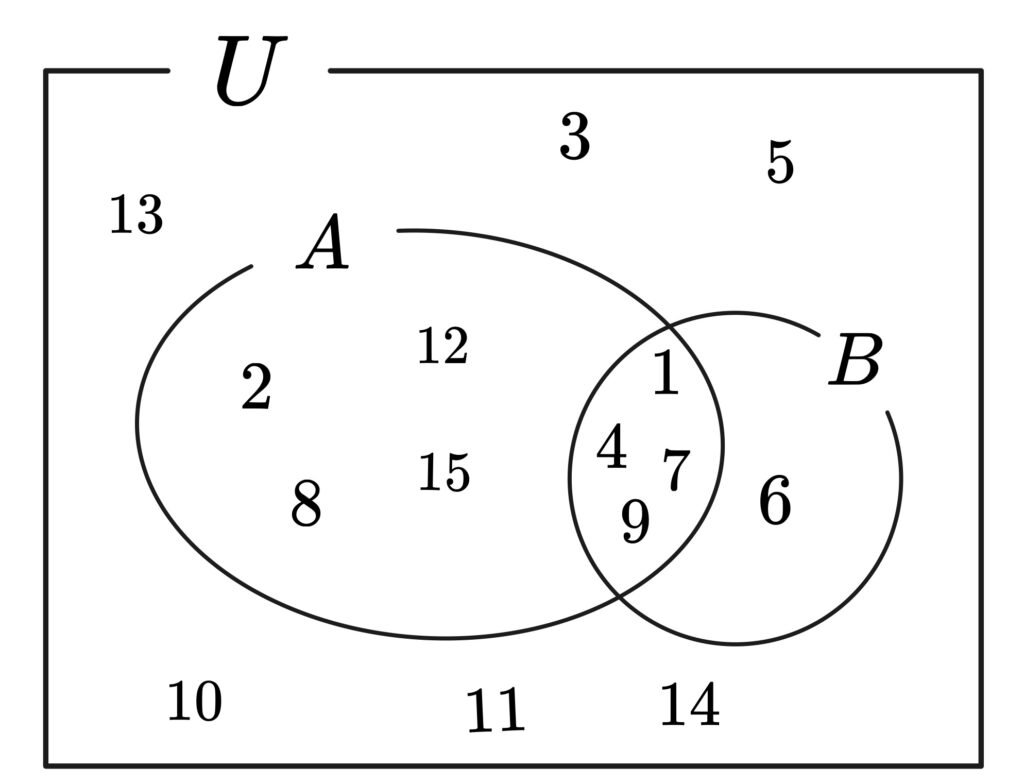
\((1)\)~\((4)\) くらいまではもうわかりそうですね。
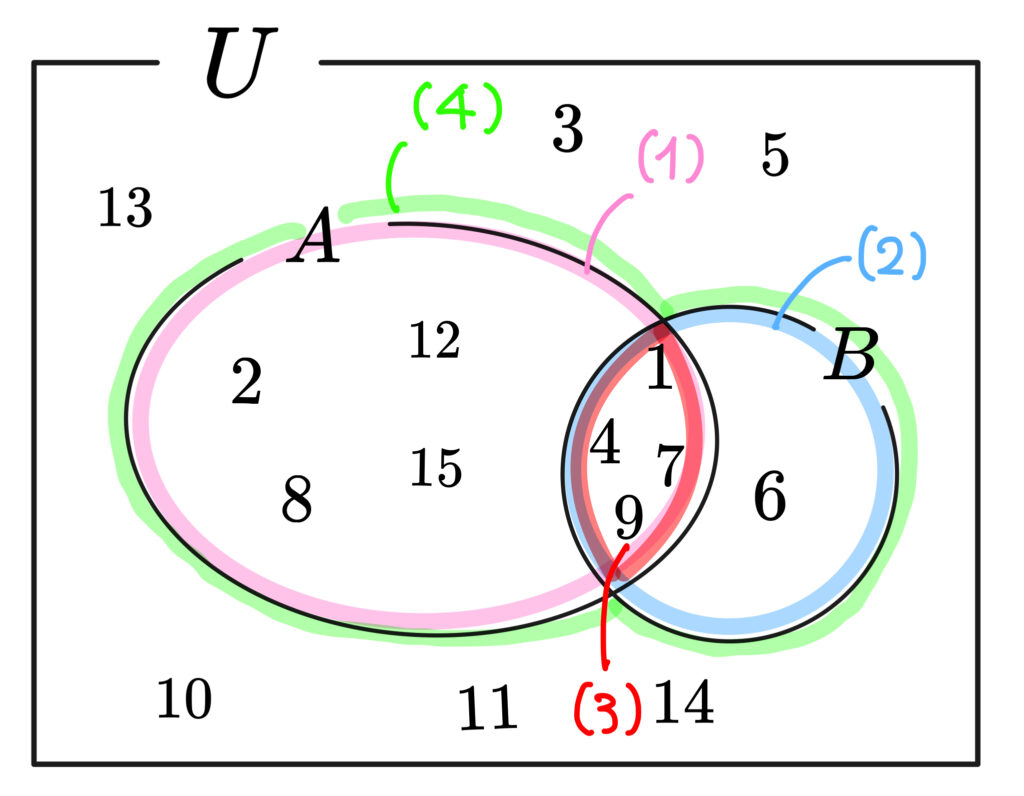
\(n(■)\) の記号は■の要素の個数を答えればいいんですよね。
つまり、、、
\((1)~~n(A)=8\)
\((2)~~n(B)=5\)
\((3)~~n(A \cap{B})=4\)
\((4)~~n(A \cup{B})=9\)
OKです。
ではつぎに\((5),(6)\) をやってみましょう。
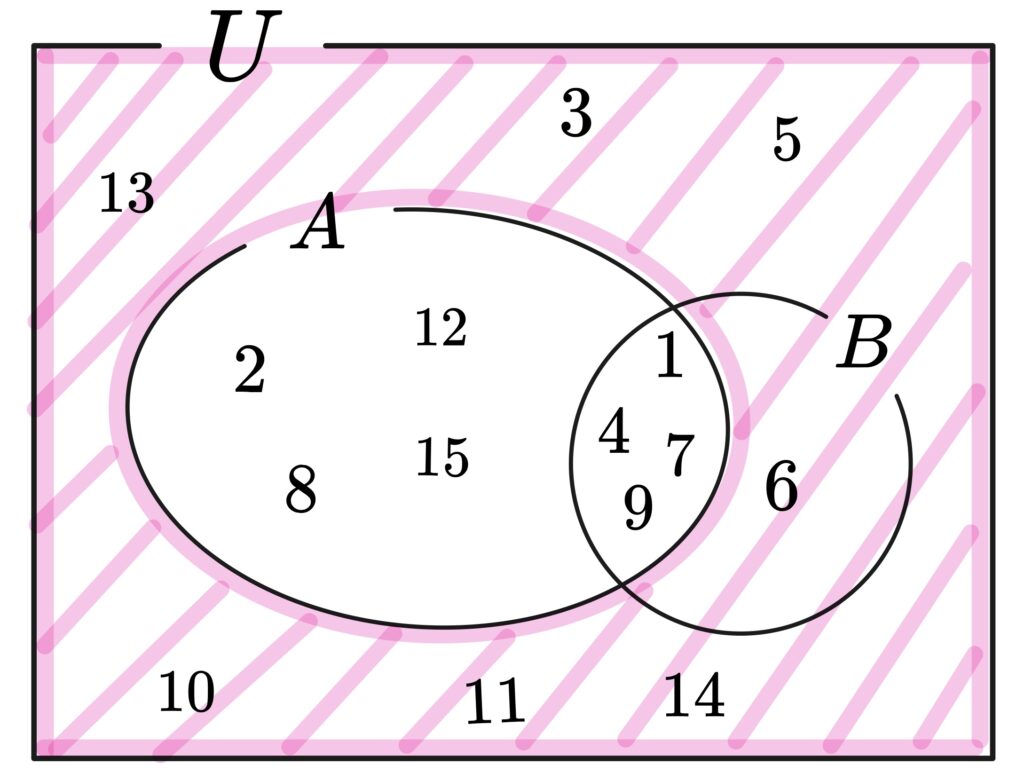
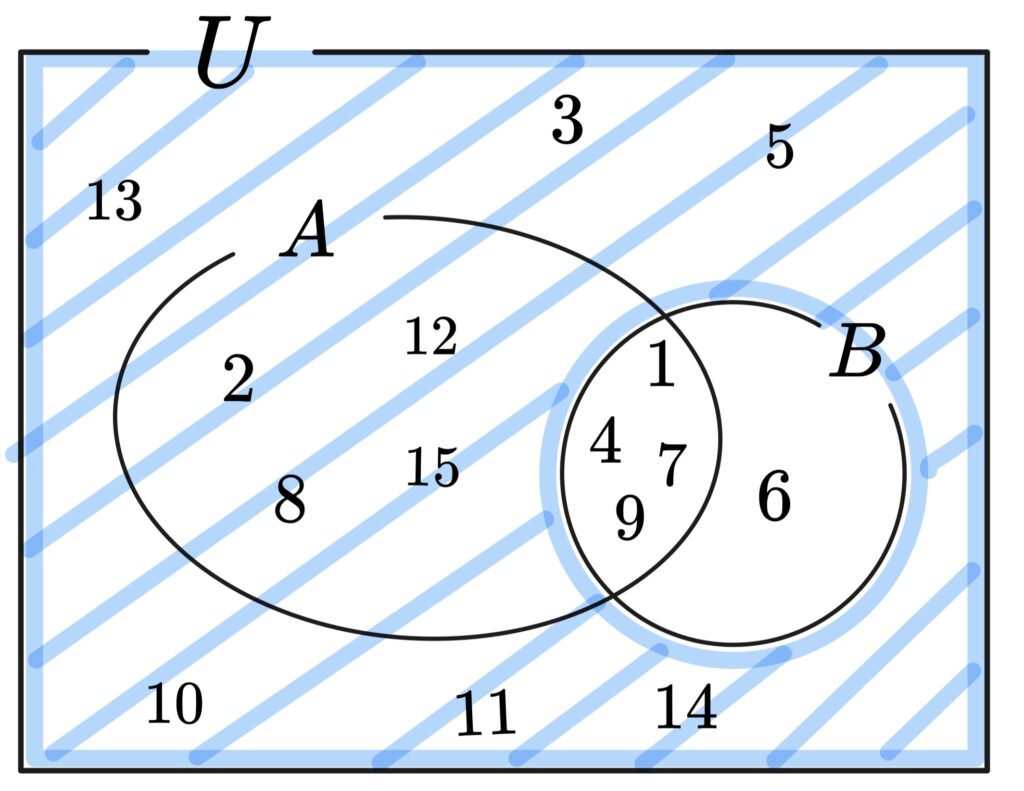
\(n(\overline{■})\) の記号は「\(■\) でない」要素の個数だから、、、
\((5)~~n(\overline{A})=7\)
\((6)~~n(\overline{B})=10\)
ということですね。
正解です。
では最後に\((7)\)~\((9)\) もやってみましょう。
\((7)\) の\(n(\overline{A \cup{B}})\) は「\(A \cup{B}\) でない」部分だから、
\((4)\) の問題の残りの個数を答えればいいので、
\(n(\overline{A \cup{B}})=6\) です!
\((8)\),\((9)\) はちょっと難しいな。。
ヒントとして、下のベン図を見てみましょう。
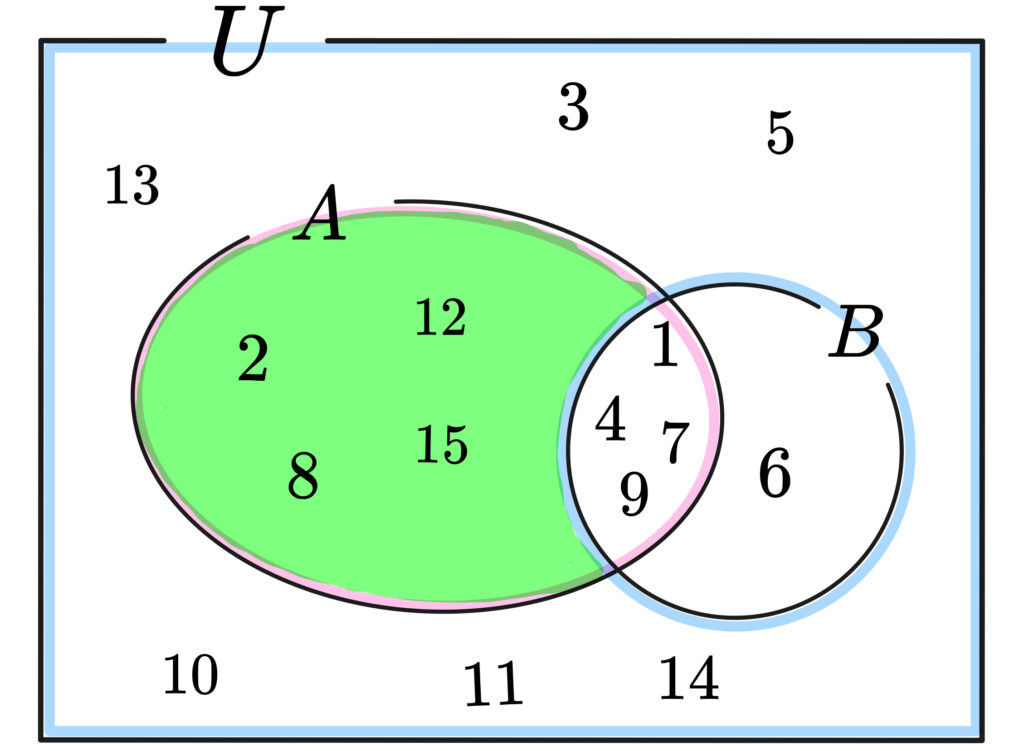
先生!これは大ヒントじゃないですか??
\((8)\) \(A \cap{\overline{B}}\) は「\(A\)と\(B\)でない の共通部分」だから
\(\{2,8,12,15\}\)が入っているエリアですね!
\(n(A \cap{\overline{B}})=4\) です。
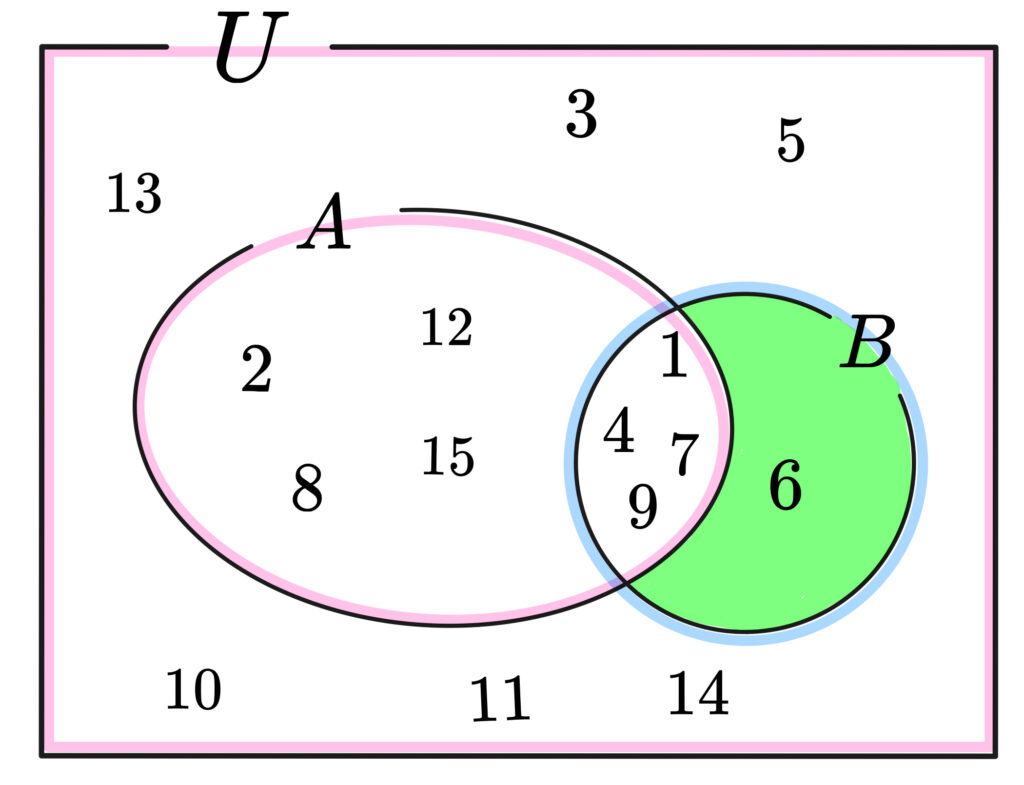
\((9)\) \(\overline{A} \cap{B}\) は「\(A\)でないと\(B\) の共通部分」だから
\(\{6\}\)が入っているエリアです。
\(n(\overline{A} \cap{B})=1\) で合ってますか?
大正解!ヒントを出しすぎましたかね?
でもこうやってベン図でみれば難しくありませんよね。
よし。応用的な集合と要素の個数にも取り組んでみます!




コメント