先生~~。ベン図が3個になったら少し難しいです。
この問題どうやって解きますか??
問題
\(1\) から\(100\) までの整数のうち,次のような数は何個あるか。
\((1)~~2,3,7\) の少なくとも1つで割り切れる数
\((2)~~2\) では割り切れるが、\(3\)で\(7\)でも割り切れない数
n浪君。まずは、
\(2\) で割り切れる集合を\(A\), \(3\) で割り切れる集合を\(B\),
\(7\) で割り切れる集合を\(C\) としましょう。
はい。ついでに
\(A \cap{B} ,~B \cap{C} ,~C \cap{A} ,~A \cap{B}\cap{C}\)
のそれぞれの要素をまとめてみました!

n浪君。気が利きますね~。
じゃあこれらの集合の要素の個数をベン図にまとめてみましょう!
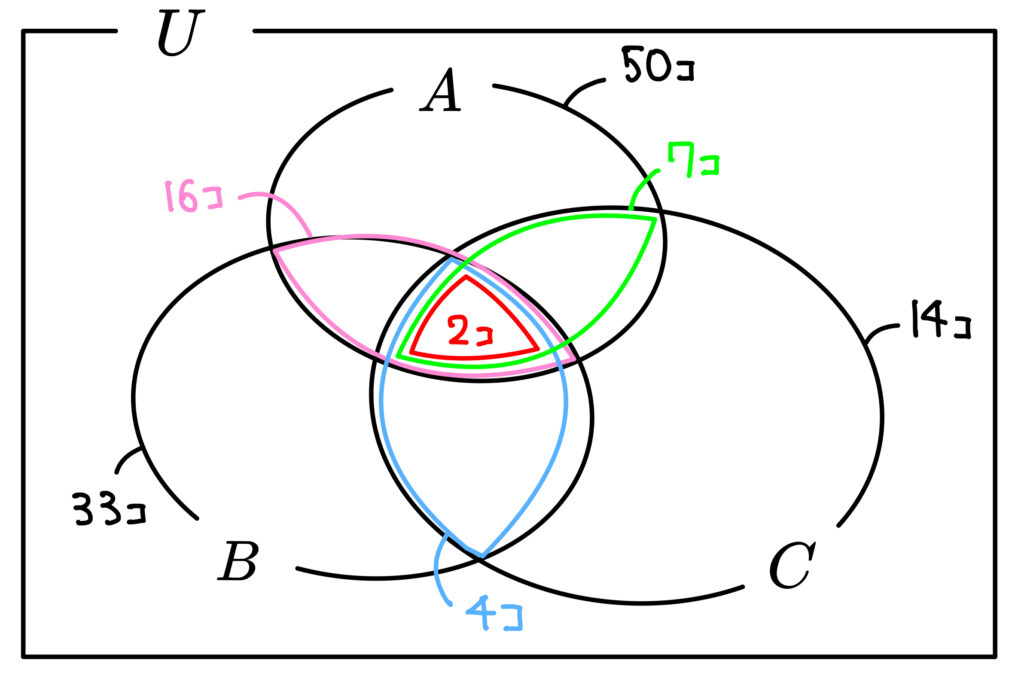
こう書くと見やすいですね!
あとは空いている部分の個数を埋めてみます。
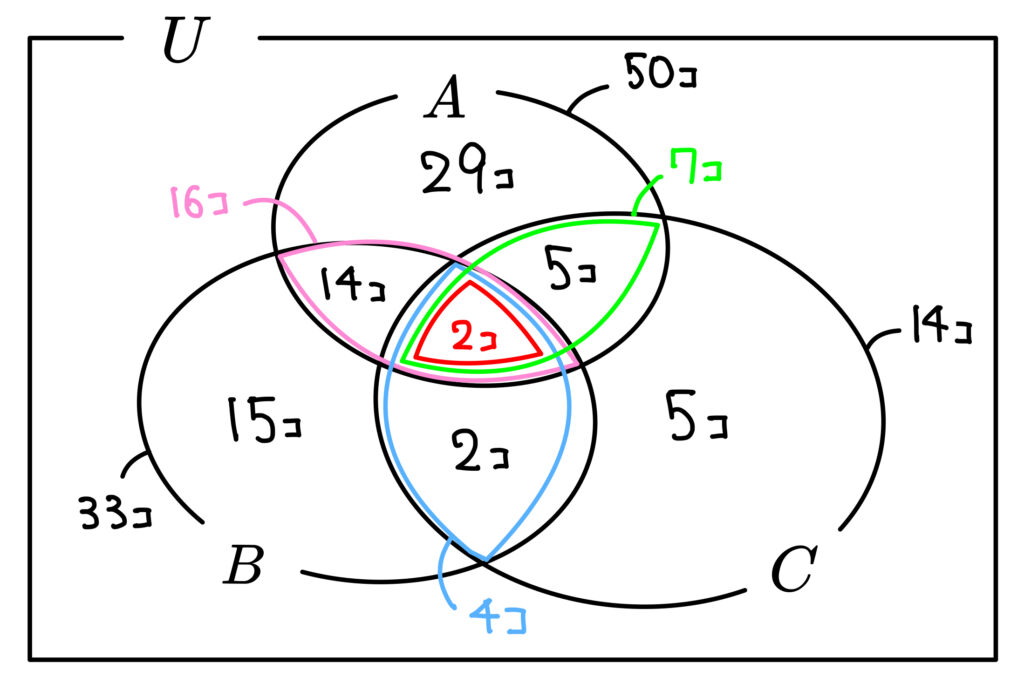
さぁ準備完了ですね。
\((1)~~2,3,7\) の少なくとも1つで割り切れる数
\((2)~~2\) では割り切れるが、\(3\)で\(7\)でも割り切れない数
の個数はどうなるでしょう。
\((1)\) はベン図の各部分の個数を足せばいいので
\(29+15+5+14+2+5+2=72\) (個)ですね。
OKです。
では\((2)\) はどうでしょう?
\(A\) に入っていて\(B\)にも\(C\)にも入っていなければいいから
あっ!もう出てますね。\(29\) (個)です!
大正解!
n浪君。調子いいですね!




コメント