先生!今日は組合せの記号 \(\rm{C}\) について
もっと詳しく教えてくれるんですよね?
はい。ではまず \(\rm{C}\) の計算を階乗のみで表します。
n浪君。例えば \(_7\rm{C}_4\) の計算はどうなりますか?
\(_7\rm{C}_4=\dfrac{7\cdot6\cdot5\cdot4}{4\cdot3\cdot2\cdot1}=35\)
ん?階乗のみで表せるんですか?
ちょっとイメージがわかないなぁ…。
いったん次を見てください。
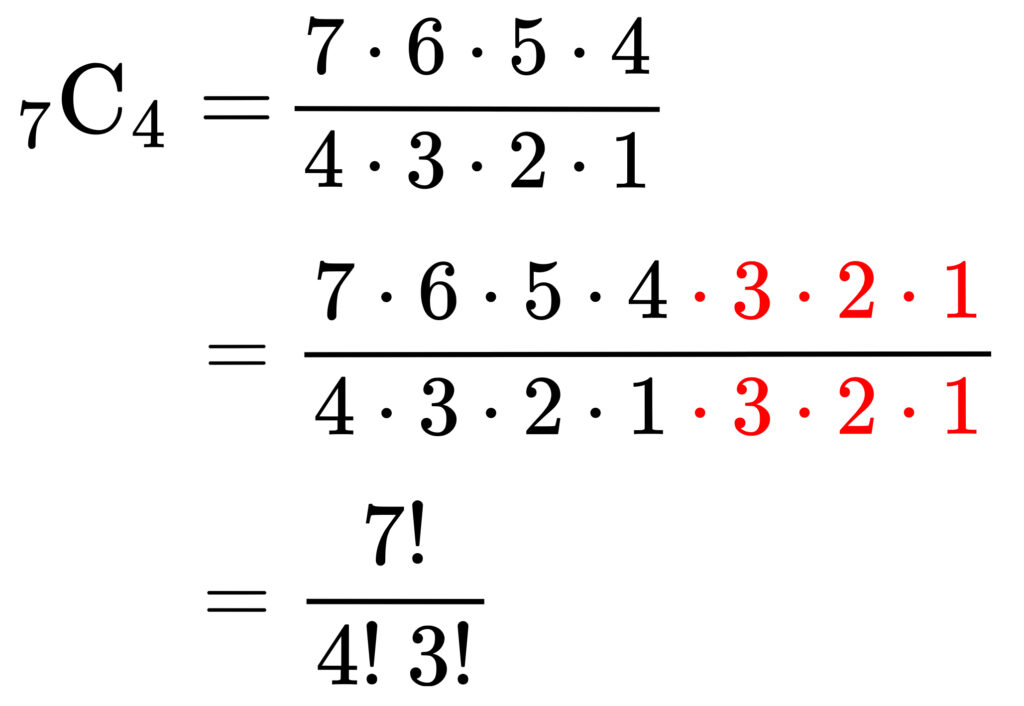
たしかに階乗の記号だけで書けてますね。
なるほど。
分母と分子に\(\color{red}{3\cdot2\cdot1}\)を掛けているのかぁ。
具体例で見るとそんなに難しくないでしょう?
例えば\(_8\rm{C}_3\) ならどうでしょうか?
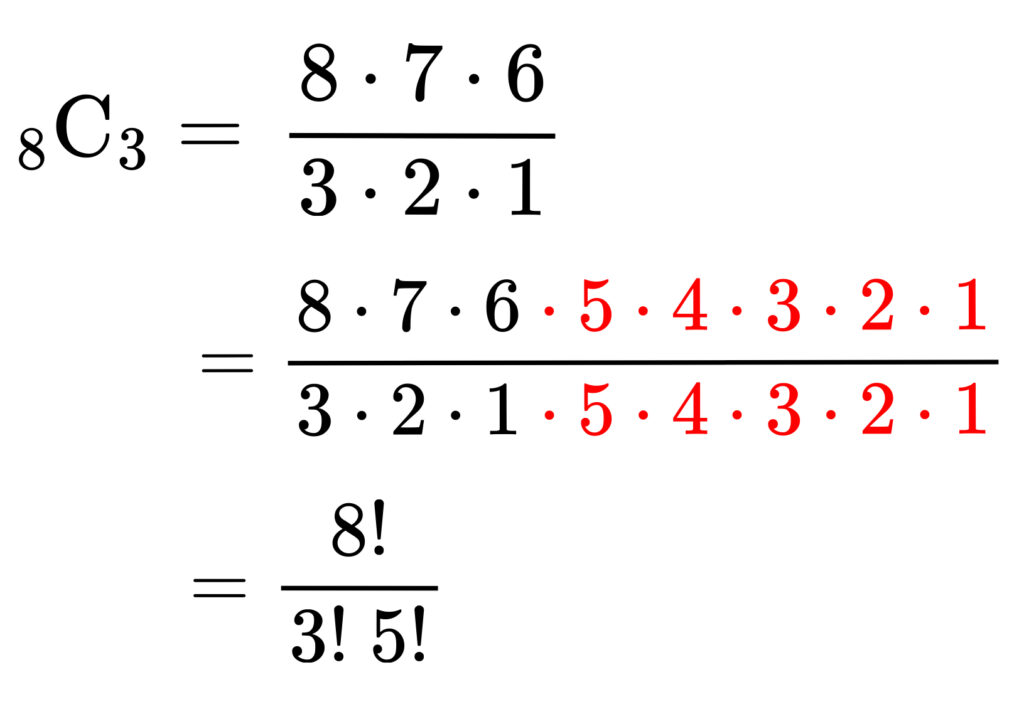
変形できるようになりました!
あと気づいたんですが、これって\(_8\rm{C}_5\)
も同じ結果になりませんか?
n浪君。いいところに気づきましたね。
たしかに、\(_8\rm{C}_5=\dfrac{8!}{5!\,3!}\)で\(_8\rm{C}_3\) と一致します。
これも重要な性質の1つなんです。ではまとめてみましょう。
1. \(_n\mathrm{C}_r=\dfrac{n(n-1)(n-2)\cdots\cdots(n-r+1)}{r(r-1)\cdots\cdots3\cdot2\cdot1}\)
\(~~~~~\)特に\(~~_n\mathrm{C}_1=n,~_n\mathrm{C}_n=1\)
2. \(_n\mathrm{C}_r=\dfrac{n!}{r!(n-r)!}\) また, \(_n\mathrm{C}_0=1\) と定める。
\(0\leqq{r}\leqq{n}\) とする。
このとき, \(_n\mathrm{C}_r\,=\,_n\mathrm{C}_{n-r}\) が成立する。
とくに②については,先ほどn浪君が気づいた性質です。
8個の中から5個選ぶ方法は、余り物の3個の選び方と同じ
といった感覚で\(_8\rm{C}_5~=~_8\rm{C}_3\)と思っていいでしょう。
わかりました!
組合せの記号\(\rm{C}\) は何かと便利そうですね~。




コメント