先生!今日は順列 の記号 \(_n\rm{P}_r\) の意味について
教えてください。
n浪君。実は \(_n\rm{P}_r\) の計算はとても簡単なんです。
次の問題を見てみましょう。
5個の異なる文字\(A,B,C,D,E\) について以下の場合の数を求めよ。
\((1)~~\) 3つの異なる文字を選んで1列に並べる方法は何通りあるか。
\((2)~~\) 5つすべてを選んで1列に並べる方法は何通りあるか。
これは前回学んだ順列の問題でやりましたね。
樹形図を考えればいいから…
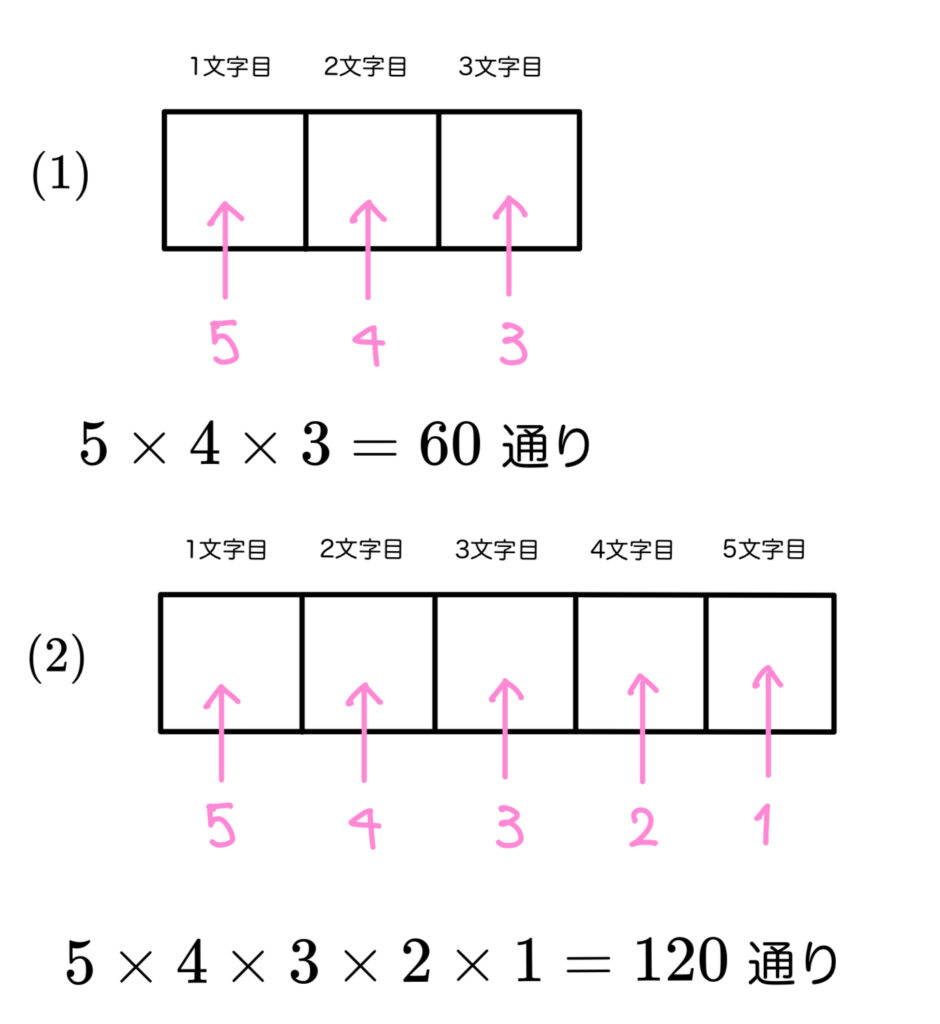
OKです。ちゃんと理解できているようですね。
実はこの計算の中に順列の記号 \(_n\rm{P}_r\)は隠れています。
え?どこに隠れているんですか?
こちらを見てください。
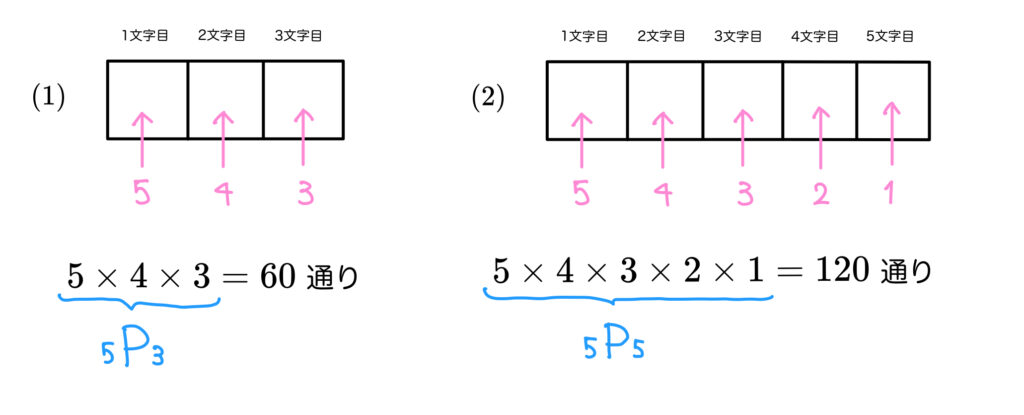
ん?この\(\rm{P}\)の前後の小さい\(5\) とか\(3\)
の数字は何に対応しているんだろう?
\((1)\) は5個の異なる文字から3つ選んで並べる
\((2)\) は5個の異なる文字から5つ選んで並べる
順列の数を数えています。
まとめるとこのようになります。
異なる \(n\) 個のものから,\(r\) 個の異なるものを選び1列に並べたものを,
「\(n\) 個から\(r\) 個取り出して並べた順列」といい,その個数を \(_n\rm{P}_r\) で表す。
じゃあ6個の異なるものから4つ選んで並べたときの場合の数は
\(_6\rm{P}_4=6\times5\times4\times3=360\) という計算となるわけか~。
では\(_n\rm{P}_r\) の計算式はどうなるんですか?
少し難しいですが,いままでの問題と同じように考えましょう。
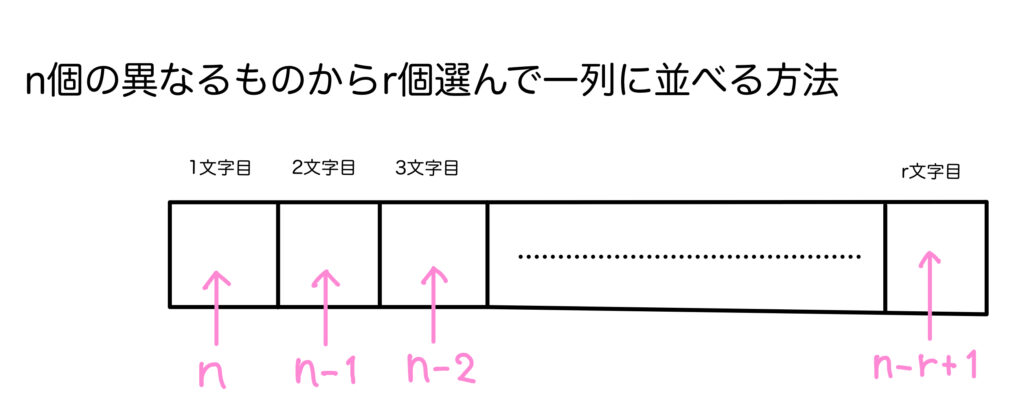
\(_n\mathrm{P}_r={n}\times(n-1)\times(n-2)\times\cdots\times(n-r+1)\) と計算される。
特に, \(_n\mathrm{P}_n={n}\times(n-1)\times(n-2)\times\cdots\times{2}\times{1}\) である。
見た目は難しいですが、計算方法は樹形図のとおりですね。
じゃあこの問題は簡単ですね!
次の値を計算せよ。
\((1)~~_4\rm{P}_3~~~~~~~~(2)~~_5\rm{P}_2~~~~~~~~(3)~~_{10}\rm{P}_1\)
\((1)~~_4\rm{P}_3=4\times3\times2=24\)
\((2)~~_5\rm{P}_2=5\times4=20\)
\((3)~~_{10}\rm{P}_1=10\)
全部合ってますか?
全問正解です。ただこれはただの計算記号なので、
必ず使わなければいけないわけではないのです。
確かに、ただの積の法則ですもんね!




コメント