先生!場合の数を勉強していたら「和の法則・積の法則」
っていうよくわからないのが出てきました…。
結局、和の法則と積の法則はどのように使い分けるんですか?
教科書にはこのように書いています。
2つの事柄\(A,B\)は同時に起こらないものとする。
\(A\) の起こり方が\(a\) 通りあり、\(B\) の起こり方が\(b\) 通りあるとすると、
\(A\) または\(B\) が起こる場合は\(a+b\) 通りある。
事柄\(A\)の起こり方が\(a\) 通りあり、そのおののの場合について、事柄\(B\) の起こり方が\(b\) 通りあるとすると、\(A\) と \(B\) がともに起こる場合は\(ab\) 通りある。
わかった!つまり2つの事柄\(A\) と\(B\) について、
同時に起こらないなら和の法則で
同時に起こるなら積の法則を使う
ってことですか?
勘違いしやすいところですが、そうではありません。
1つ問題を見てみましょう。
大小2個のサイコロを投げるとき、次の場合は何通りあるか。
\((1)~~\)目の和が\(5\) または \(6\)
\((2)~~\)目の和が\(5\) または目の積が\(6\)
やってみます!
サイコロ2個の問題は表を書いてみればいいですね。
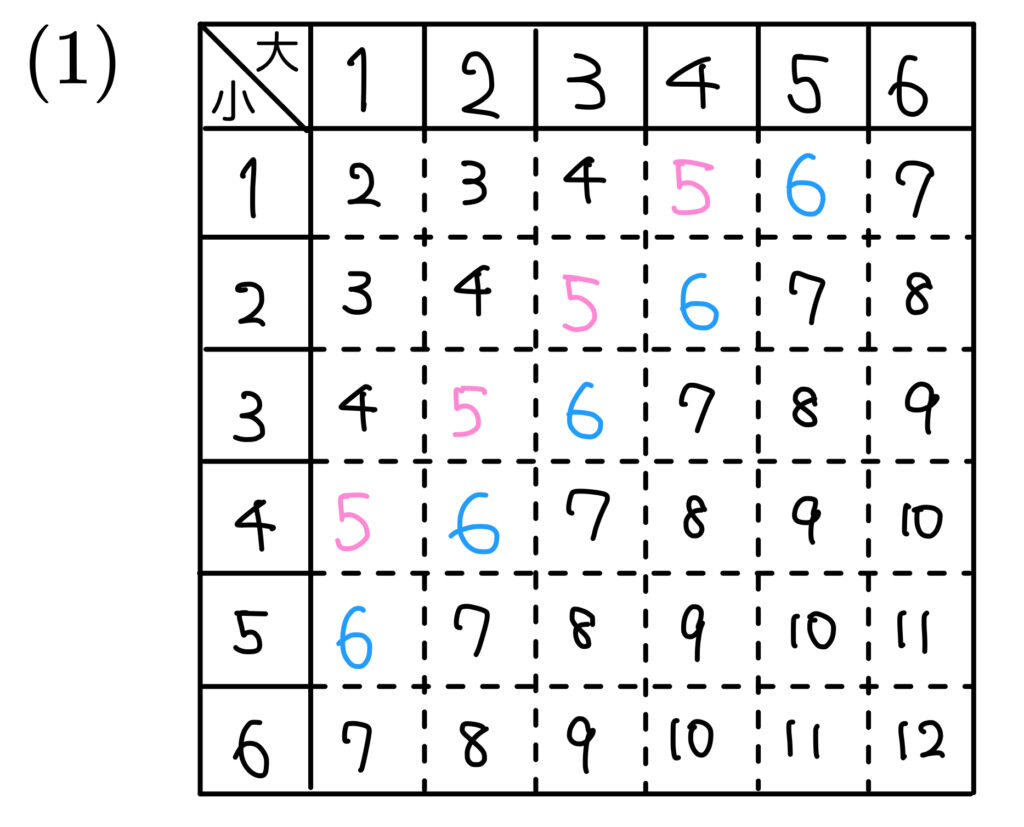
\((1)\) は
4通りと5通りで合わせて\(9\) 通りですね!
OKです。\((2)\) はどうなるでしょう?
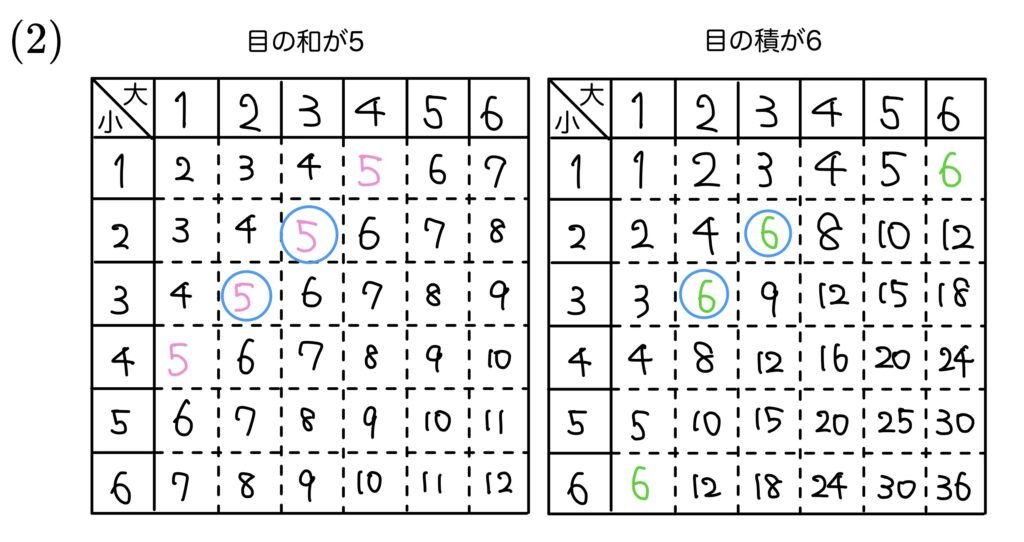
\((2)\) は
目の和が5になるのが4通り
目の積が6になるのが4通り
なんですが、\((2,3),(3,2)\) の2通りの目では
どちらの事柄も起こります!
なので\(4+4-2=6\) 通りになりますね。
はい正解です。
ここで気を付けるべきは、
事柄\(A\) と事柄\(B\) に分けたとき
\((1)\) では同時に起こらないので、そのまま足した。
\((2)\) では同時に起こる部分があるので、引く部分がある。
ということです。
特に\((1)\) の2つの事柄は排反と言ったりします。
え?じゃあ同時に起こる場合に積の法則
を使うっていうのは間違いなんですか?
その考え方は間違いです。
1つ積の法則を使う問題をやってみましょう。
大小2個のサイコロを投げるとき、大きいサイコロで偶数の目が出て小さいサイコロで2以下の目が出る目の出方は何通りあるか。
とりあえず数え上げてみますね。
樹形図を使ってみるとよさそうだな。
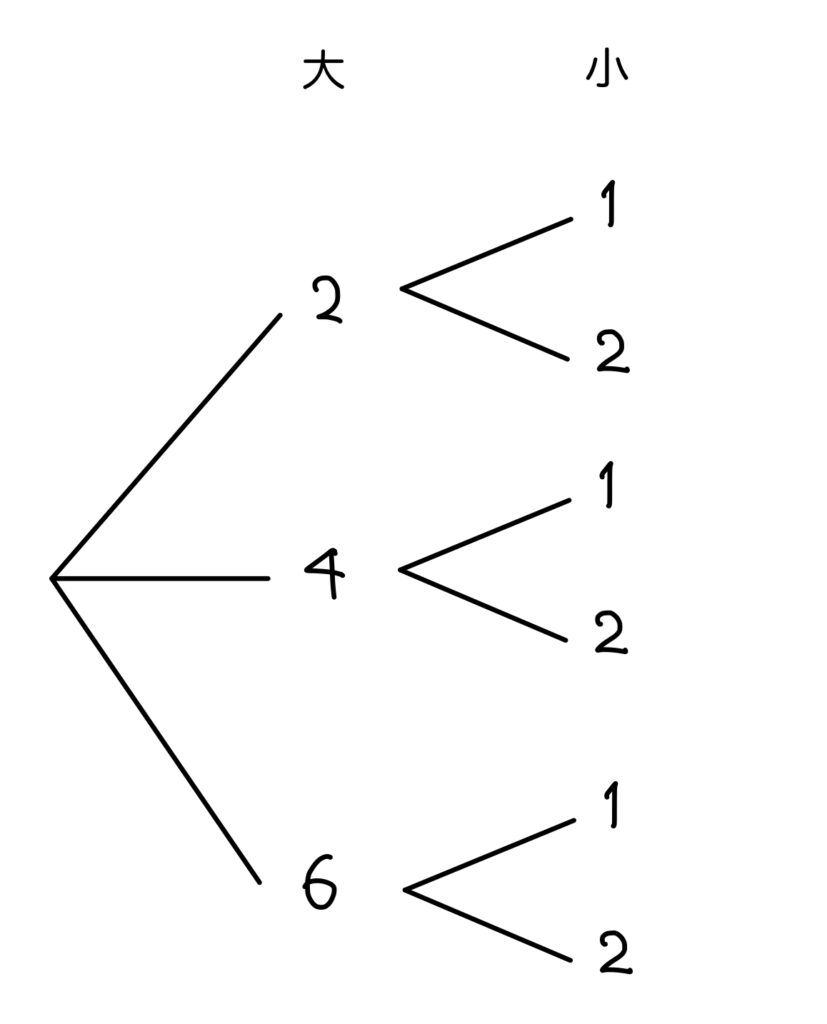
簡単でした!\(6\) 通りです。
OKです。
この問題のポイントは
大きいサイコロの3通りの目に対して、
それぞれ小さいサイコロの2通りの目
があるので、\(3\times2=6\) 通りと計算できることです。
樹形図を考えたとき、同じ枝の本数ずつ付く場合には
積の法則で掛け算すればいいんですね~。
この2問を通じて、n浪君に伝えたいのは、
和の法則 or 積の法則っていう対比はおかしいんです。
うーん…。
教科書を読んでると、そういう風に勘違いしていました。
先生!最後にまとめをお願いします。
わかりました。
私なりにまとめたものを見てください。
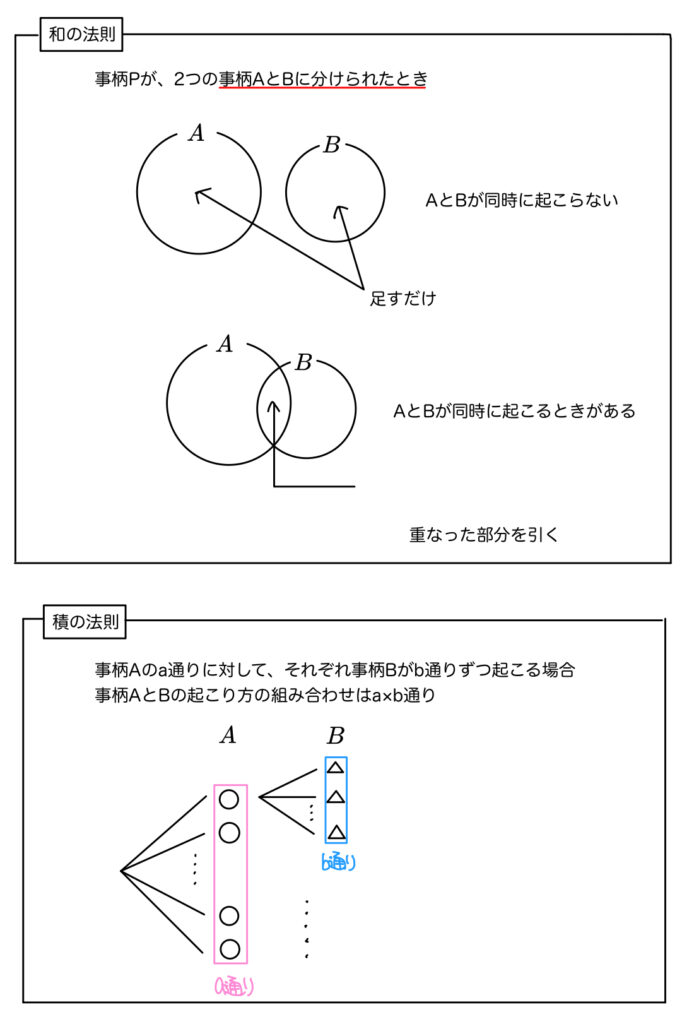
和の法則は1つの事柄が2つの事柄に場合を分けられたときに考える。
積の法則は1つの場合を考える上での計算に過ぎないんですね。
はい。ですから、
和の法則や積の法則に固執しない方がいいかもしれませんね。




コメント