先生!順列の問題で解けない問題があるのですが、
これはどうやって考えるんでしょうか?
男子 \(3\) 人 女子 \(5\) 人が1列に並ぶとき、次のような並び方は何通りあるか。
\((1)~~\)\(8\) 人が並ぶ方法
\((2)~~\)男子 \(3\) 人が隣合う
\((3)~~\)男子どうしが隣合わない
これは定番の問題ですが、重要な考え方が詰まっています。
\((1)~\)は大丈夫ですね?
階乗の計算をすれば簡単ですね。
\(8!=40320\) 通りです!
先生が覚えた方がいいって言うんで覚えましたよ~。
それでは\((2)\) の問題
「男子 \(3\) 人が隣合う」場合を解いてみましょう。
ポイントは隣り合うものをカタマリとして考えることです。
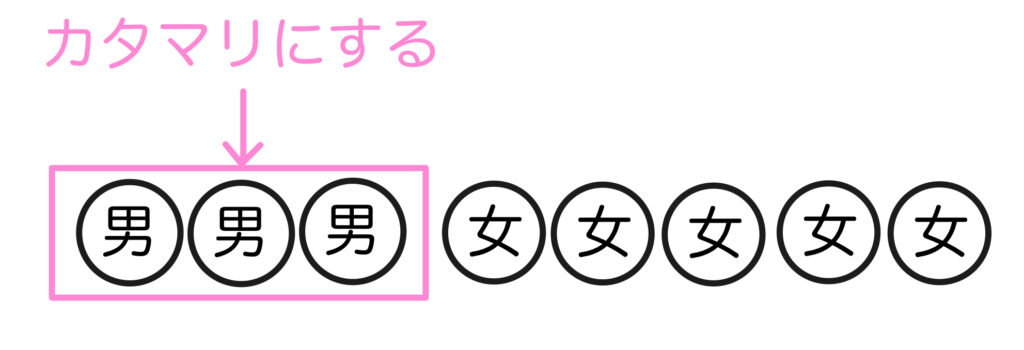
バラバラにならないようにカタマリにしておくんですね。
そうすると男子3人の1組と女子5人の合計6コを並べて…
\(6!=720\) 通りですか?
残念。まだ男子3人の並び方を考えてませんよね?
n浪君が答えた \(720\) 通りは、それぞれ男子3人の並び方によって異なる並びとなります。
そっか!
カタマリの中の並びもあるんだった。
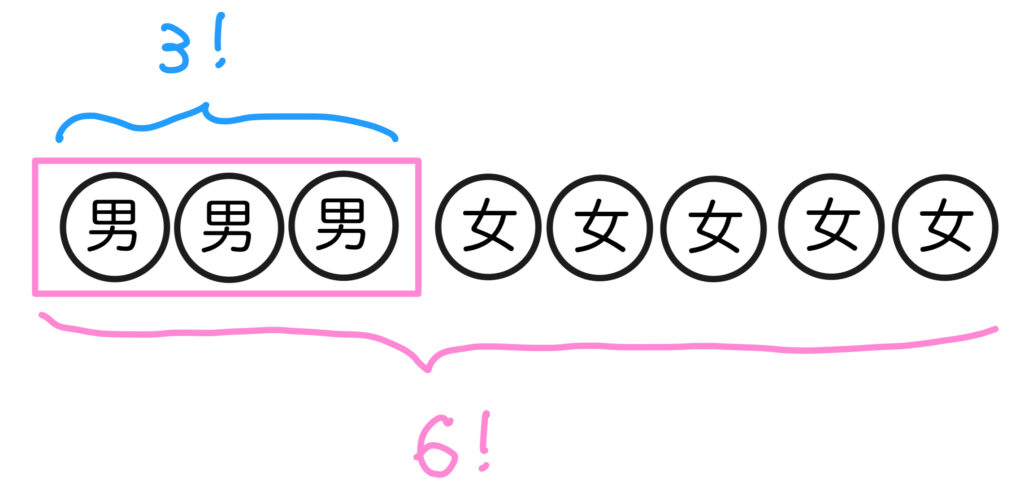
つまり…
\(6!\times{3!}=720\times{6}=4320\) 通りですね!
正解!そういうことです。
では\((3)\)の問題
「男子どうしが隣合わない」場合も考えてみてください。
うーん…。
とりあえず何パターンか調べてみたんですが…。
全部書き出していくのは大変ですね。
この「隣合わない」のポイントは男子が入れるスキマを考えることです。
確かに3人の男子はそれぞれ必ず女子のスキマに入りますね~。
このスキマが何通りあるか調べるのか!
はい。まずは女子5人を並べると、6ヶ所のスキマがあります。
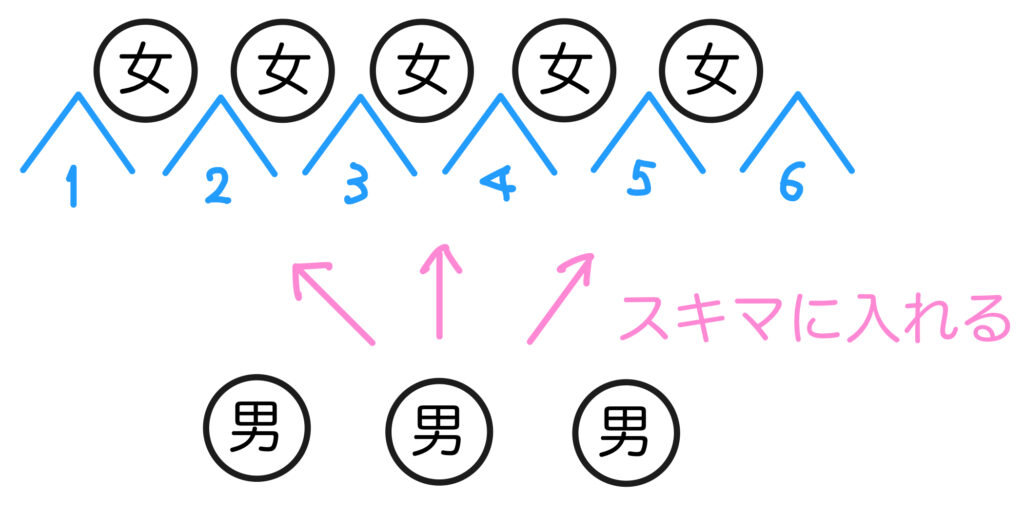
男子3人が入れるスキマのパターンは何通りあるでしょう?
1人目の男子が6通り,2人目が5通り,3人目が4通り….
てことは\(_6\mathrm{P}_3=6\times{5}\times{4}=120\) 通りか!
OKです。あとは\(120\) 通りそれぞれに女子5人の並びがあることに注意してください。
わかりました。
\(_6\mathrm{P}_3\times{5!}=120\times{120}=14400\) 通りです!
よくできました。
これで順列の問題がたくさん解けるようになりましたね。




コメント