先生!今日は1次不等式について勉強したいです。
わかりました。
n浪君。ここで大事なのは、まず不等式の性質です。
以下をご覧ください。
\(1.~~~A<B~\)ならば\(A\pm{C}<B\pm{C}\)
\(2.~~~A<B~\)かつ\(C>0\) ならば\(AC<BC,~~\dfrac{A}{C}<\dfrac{B}{C}\)
\(3.~~~A<B~\)かつ\(C<0\) ならば\(AC>BC,~~\dfrac{A}{C}>\dfrac{B}{C}\)
え~と…。これのどのあたりが大事なんですか??
\(1.\)については大小関係がついている数に
各辺同じ数を足したり引いたりしても大小関係は変わらない
ということです。(移項ができる理由になる)
\(2.\)と\(3.\)は大小関係がついている数に
プラスのものをかけたり割ったりしても大小関係は変わらないが、
マイナスのものをかけたり割ったりしたら大小関係は逆転する。
…と言葉で説明するとこんなところです。
まぁとりあえずはこの性質に従っていけば、
1次不等式を解くことができるんですね?
そうですね。
そこまで難しくはないので、とりあえず初歩の問題をやってみましょう。
次の不等式を解け。
\((1)~~4x+6<2x-2\) \((2)~~9-x\leqq{2x-3}\)
性質1.~3.に忠実に従って解いてみます!
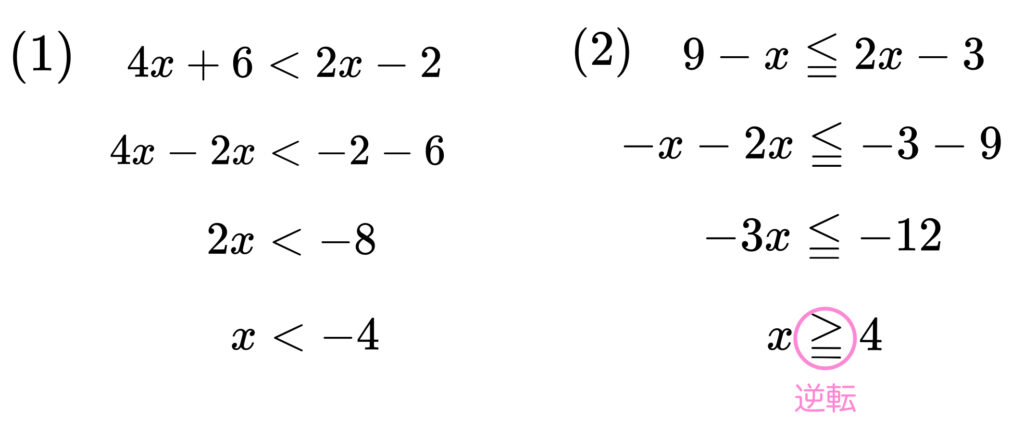
OKです。\((2)\) は最後に両辺をマイナスで割るので
不等号の向きが逆転することがポイントでした。
またはこうやってもいいのでは??

たしかに暗算で解こうとすると、
こっちの方が間違えにくいかもしれませんね~。
では最後にまとめの1問をやってみましょう!
ちょっと難しいかもしれませんが考えてください。
\(a\) は定数とする。このとき以下の不等式を解け。
\(ax<1\)
ん??難しいですか?
両辺\(a\) で割って \(x<\dfrac1{a}\) でいいんじゃないかな?
それは間違いです。
例えば \(a=-2\) ならどうでしょう?
\(-2x<1\) ってことだから,両辺マイナス2で割って…
あっ、不等式が逆転して\(x>-\dfrac12\) だ。
そうですね。
この問題は定数 \(a\) の値によって場合が変わるんです。
さらに \(a=0\) のときはどうなるでしょう??
\(0\cdot{x}<1\) ってことだから、
\(0<1\) となって…あれ?これはなんだ?
\(0<1\) は \(x\) が消えていて見づらいですが、
\(0\cdot{x}<1\) はどんな \(x\) で成立するでしょう?
先生!これって \(x\) に何を代入しても左辺は0になっちゃいますよ?
そうですね。
ということは\(x\) はなんでもいいことになりませんか?
つまりこの場合はすべての実数 \(x\) で成り立つんです。
なるほど~。ちゃんと考えれば理解できました。
では答えはこうですね!

正解です!
これができてしまえばもう大丈夫でしょう。




コメント