先生!
今回のテーマは「2次不等式≪接する・浮く≫」ですね。
ところで、接する?浮く?って何ですか?
n浪君。接する・浮くっていうのは
2次方程式と2次関数のグラフでやったアレのことです。
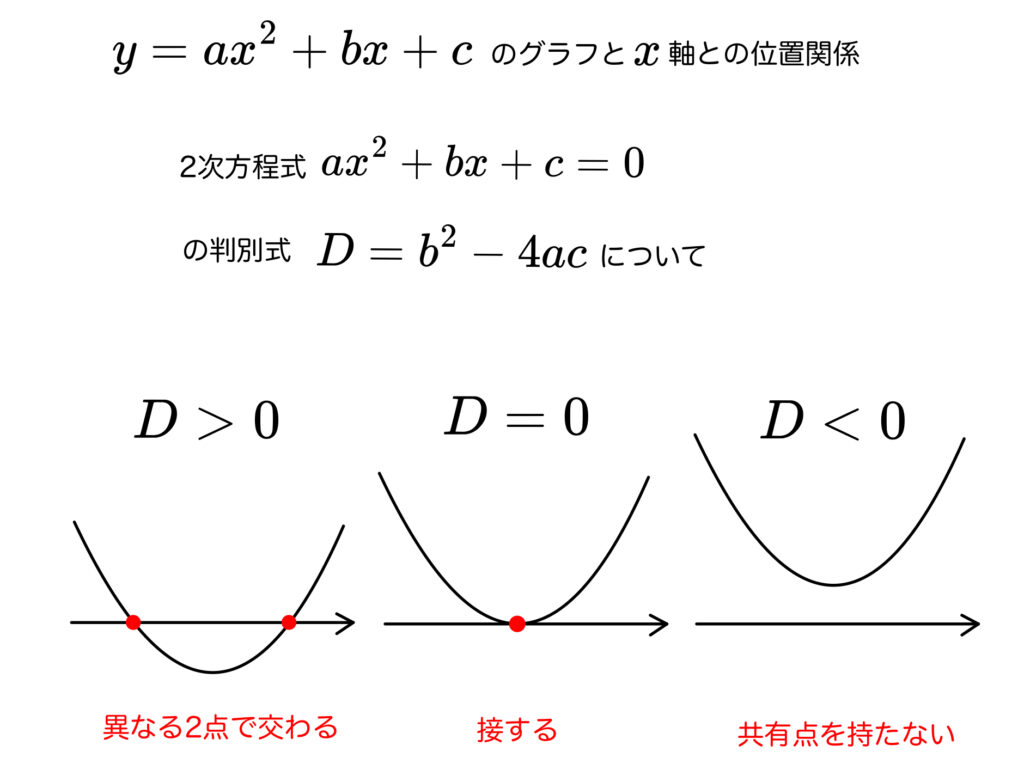
やりましたね~。
これと2次不等式が絡んでくるんですね…
はい。では1つ問題を見てみましょう。
これは接するパターンです。
次の2次不等式を解け。
\((1)~~x^2+4x+4\geqq0\) \((2)~~x^2+4x+4\leqq0\)
\((3)~~x^2+4x+4>0\) \((4)~~x^2+4x+4<0\)
全部同じように見えるんですが、違うんですね…
でも考え方は全部同じなので見てみましょう!
まずは左辺の\(x^2+4x+4\) と
\(x\) 軸との関係は以下のようになります。
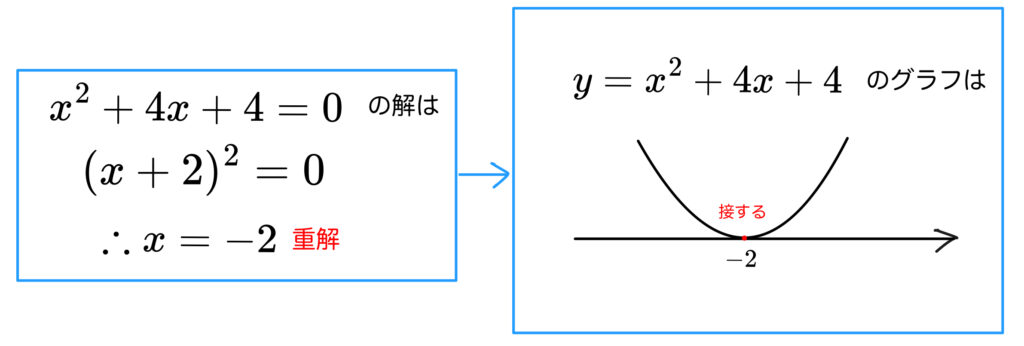
重解が得られるときは、2次関数は \(x\) 軸に接するんでしたね。
この後、どうやっていくんですか?
では一気に見てもらいましょう。
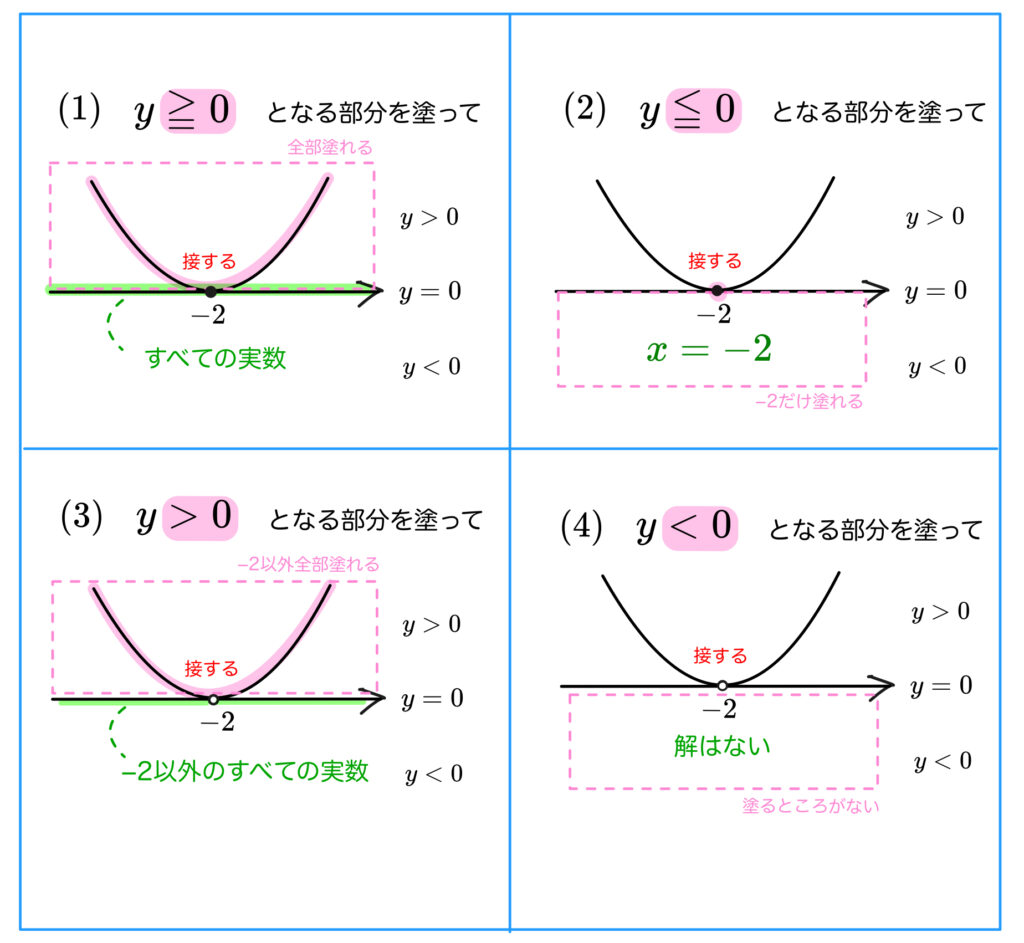
本当にグラフを見て解くんですね。
確かに、答えのパターンを覚えるのは大変そうですが、
グラフの色塗りならできそうです!
そうでしょう。ではもう1つ。
グラフが浮くパターンも考えてみてください。
次の2次不等式を解け。
\((1)~~x^2-2x+3\geqq0\) \((2)~~x^2-2x+3\leqq0\)
\((3)~~x^2-2x+3>0\) \((4)~~x^2-2x+3<0\)
さっきと同じように、
左辺の \(x^2-2x+3\) と \(x\) 軸の関係を見てみます。
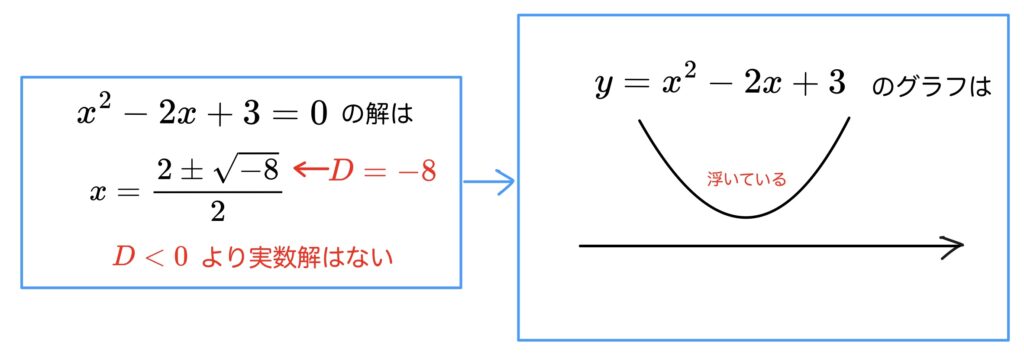
そうです。解の公式で\(\sqrt{~~}\) の中身
すなわち判別式\(D\) がマイナスなので、
n浪君が書いたようにグラフは浮きます。
あとは不等号にしたがって、色塗りしてみま~す。
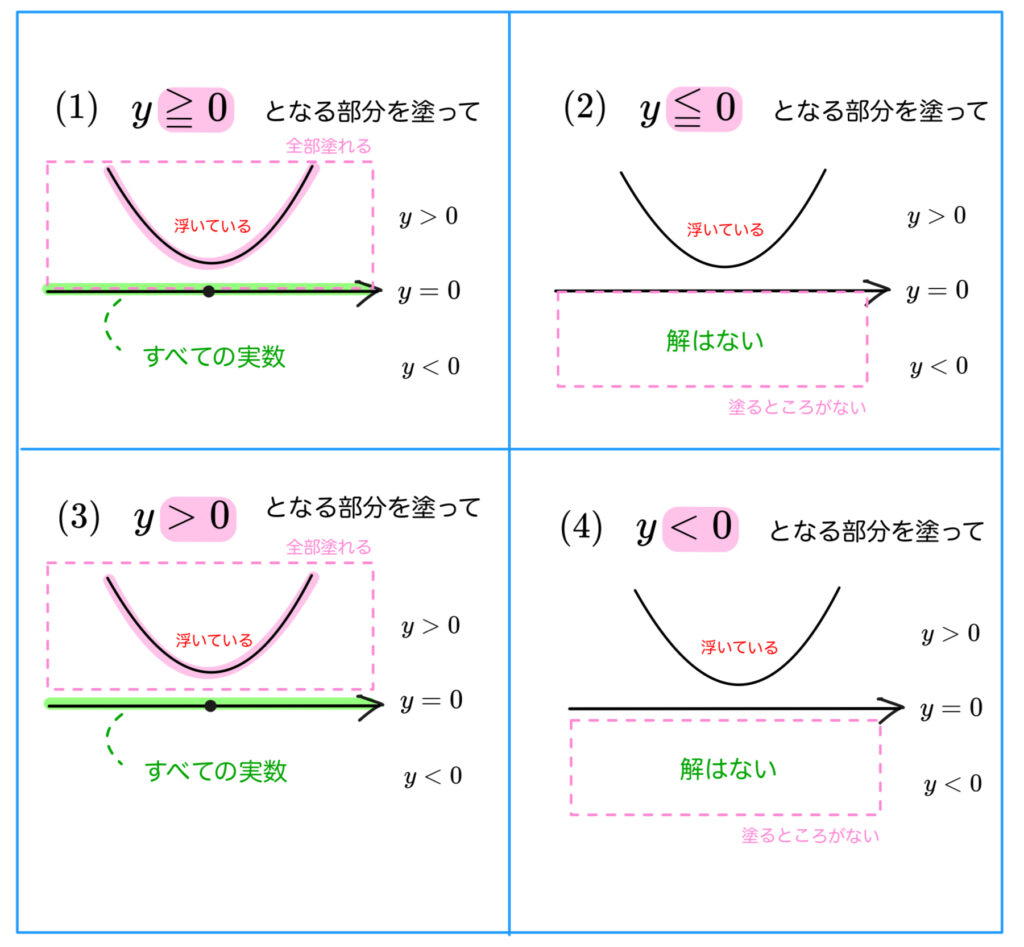
素晴らしい!
2次方程式が「解なし」だからといって、
ちゃんと不等号を見ないと間違えてしまうんです。
やっぱり、グラフで考えることが重要なんですね!




コメント