先生!2次方程式を学習してたら判別式\(D\)
というよくわからないやつが登場して…
n浪君。判別式\(D\)の式は答えられますか?
えーっと~、
\(D=b^2-4ac\) だったような…
正しいといえば正しいのですが、
はたして理解できているでしょうか。
まず2次方程式の解の公式は覚えていますか?
はい!それは覚えています!
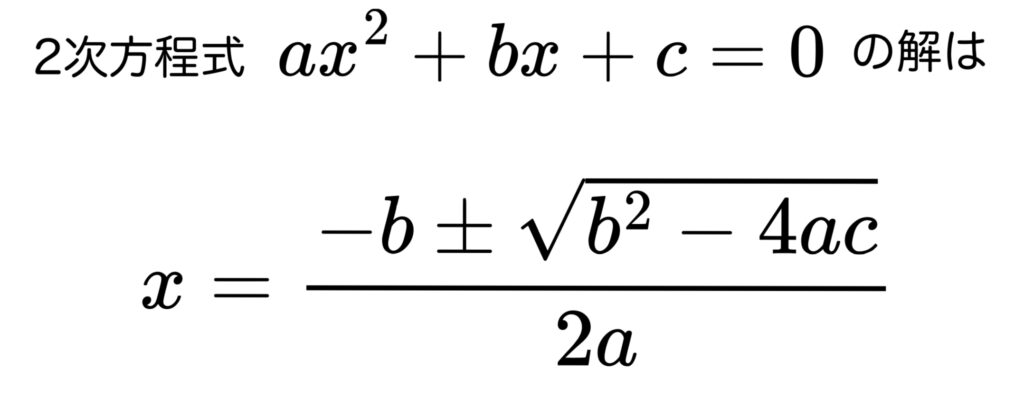
そうですね。実は判別式\(D\) はこの2次方程式の解の公式
のルートの中身そのものなんです!
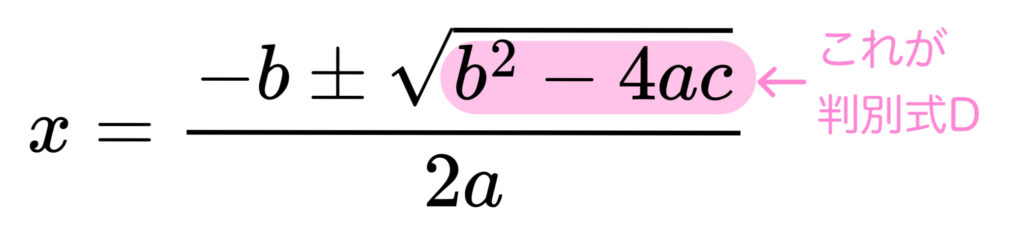
本当だ…暗記する必要なかったんですね。
で、この判別式で何がわかるんですか??
いい質問ですね。
それでは確認しましょう。
n浪君。ずばり2乗してマイナスになる数は何でしょう?
うーん…
\((-1)^2=1\) でプラスになっちゃうし…
わかりません~。正解をおしえてください!
n浪君。実は実数という世界の中には
2乗してマイナスになる数はありません!
たとえば、2乗して\(-1\)になる\(\sqrt{-1}\)
などは実数の世界に存在しないのです。
そうなんですね~。
で、それで判別式\(D\)に何の関係があるんですか?
では、まとめてみましょう。

①については\(\sqrt{~~}\) の中身がプラスで実数だから
\(\pm\sqrt{~~}\) で2つ実数解が出る。
②については\(\sqrt{0}=0\) だから
\(\pm\sqrt{0}=0\) で1つの実数解。
③については\(\sqrt{~~}\) の中身がマイナスで実数でなくなるから
実数解がでないということで合ってます?
その理解でいいと思います。
では問題をやってみましょうか。
次の2次方程式の実数解の個数を求めよ。
\((1)~~x^2+5x+1=0\)
\((2)~~3x^2-5x+3=0\)
\((3)~~9x^2+12x+4=0\)
こんな感じでどうでしょう!

いいですね。では実数解の個数を答えてください。
\((1)\) は \(D>0\) より実数解は2個
\((2)\) は \(D<0\) より実数解は0個
\((3)\) は \(D=0\) より実数解は1個
でいいですか?
OKです!判別式\(D\)を使えば、
方程式を解かなくても実数解の個数がわかるんですね。




コメント