先生!2次方程式の実数解の個数が判別式 \(D\)で
調べられるようにはなりました。
n浪君。そこまで理解できたら今日は
2次関数のグラフと\(x\) 軸との関係
について学習しましょう。
はい先生。今日も頑張ります。
それでは、まずは\(x\) 軸との共有点を求める問題をやってみましょう。
問題1
次の2次関数のグラフと\(x\) 軸との共有点の座標を求めよ。
\((1)~~y=2x^2-x-6\)
\((2)~~y=-x^2+6x-9\)
\(x\) 軸っていうことは、\(y=0\) となる点を求めるんだよな…
ってことは…

はい正解です。
ではここで共有点の個数に着目しましょう。
先生。解いた結果を見れば
\((1)\) は2個、\((2)\) は1個ってわかるじゃないですか~。
勿論そうなんですが、
座標を求めなくても個数はわかりますよね?
確かに…。
途中で解く2次方程式の解の個数がポイントってわけですね!
そうですね。こんな問題はどう考えますか?
問題2
次の2次関数のグラフと\(x\) 軸の共有点の個数を求めよ。
\((1)~~y=-2x^2+x+1\)
\((2)~~y=3x^2+4x+2\)
「共有点の個数」だけ答えればいいから…
こんな感じで考えてみればいいのかな?

正解です。
ちゃんと理解できているようですね。
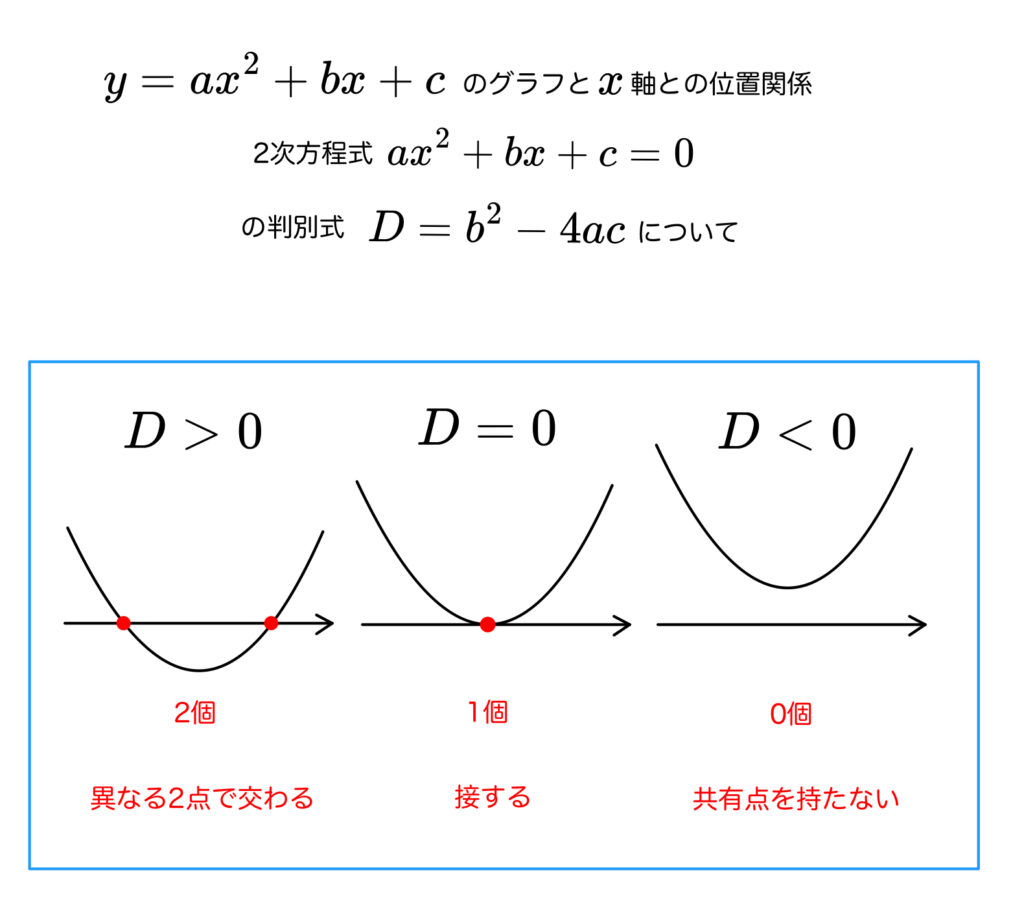
先生!つまり2次関数のグラフと\(x\) 軸との共有点の個数は
判別式\(D\) で調べられるというわけですね?
先に言われてしまいました。
このようにまとめられるので参考にしてください。
なんかモヤモヤしてたところがスッキリしました!
先生ありがとうございます。




コメント