先生!2重根号をまだ習っていないのですが、
\(\sqrt{4+2\sqrt{3}}\) ってどうやって変形出来るんですか?
n浪君。まずは以下の式を見てみましょう。
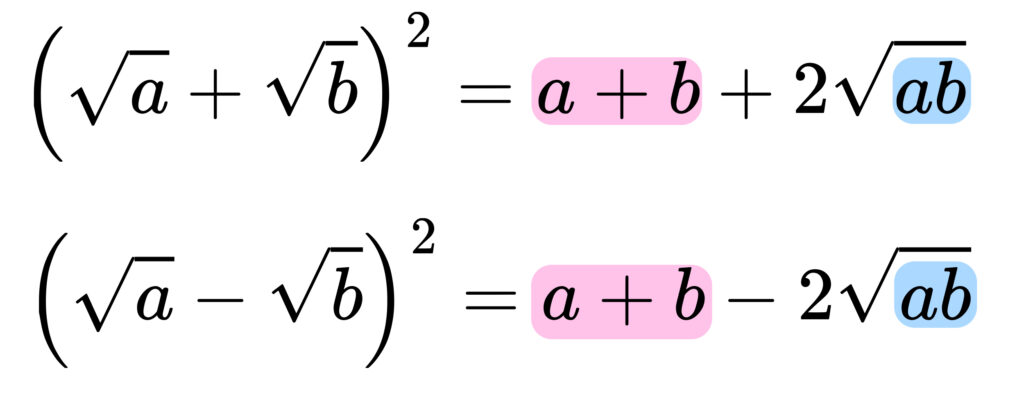
この展開式の逆をたどれば、
\(\sqrt{~~~}\)の中身に2乗の形が出てきて、ルートが外れるんですね。
そういうことです。
ですから、まずは和 \(a+b\) と 積 \(ab\) から \(aとb\) を見つけ出しましょう。
なるほど!今回は、\(a+b=4\) と \(ab=3\) だから
\(a=3,b=1\) が見つかりますね。
ということは、、、
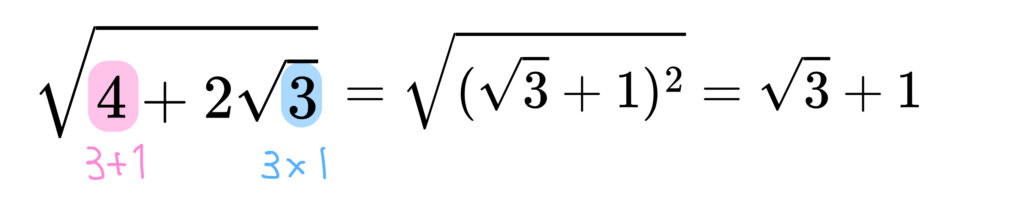
正解です。
ではもう一問、これはどうでしょうか?
\(\sqrt{9-2\sqrt{14}}\) を2重根号を外して簡単にせよ。
\(a+b=9\) と \(ab=14\) だから、、、
\(a=2,b=7\) だ!答えはこうです!
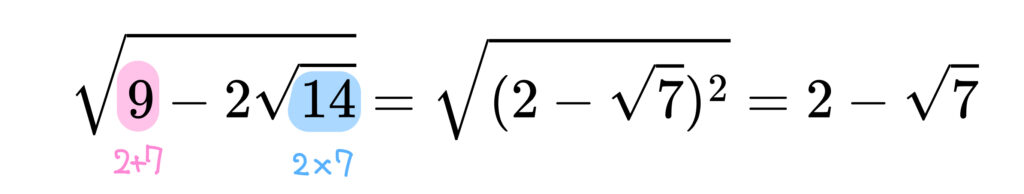
惜しい!ですが違います。
n浪君。\(\sqrt{~~~}\) を外すときに気をつけないといけないことがありましたよね??
うーん。あっ!
\(\sqrt{~~~}\) は必ず0以上の値でした。
中学校でも \(\sqrt{(-3)^2}={-3}\) とするのではなく、
\(\sqrt{(-3)^2}=3\) と習いましたね。
そうです。つまり \(2-\sqrt{7}\) ではマイナスになってしまうため、大ー小 の形で出す必要があります。
そっか。今回は\(2<\sqrt{7}\) だからこうしないとダメなんですね。
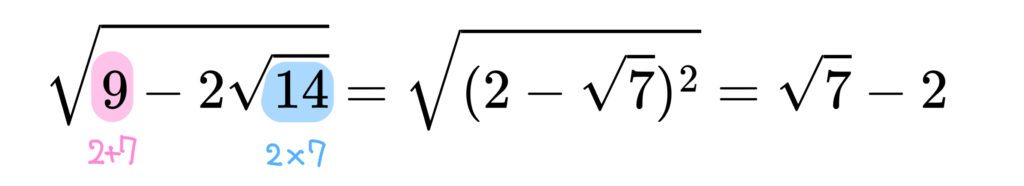
そういうことです。では、最後にもう1問チャレンジしましょう。
\(\sqrt{5-\sqrt{24}}\) の2重根号を外して簡単にせよ。
\(\sqrt{24}\) の部分が \(2\sqrt{ab}\) の形になってませんね。。
\(2\sqrt{6}\) に変形すればいいのかな?
n浪君。ナイスアイデアです!
さっきの注意もふまえて最後までやってみましょう。
先生、これでどうでしょう?
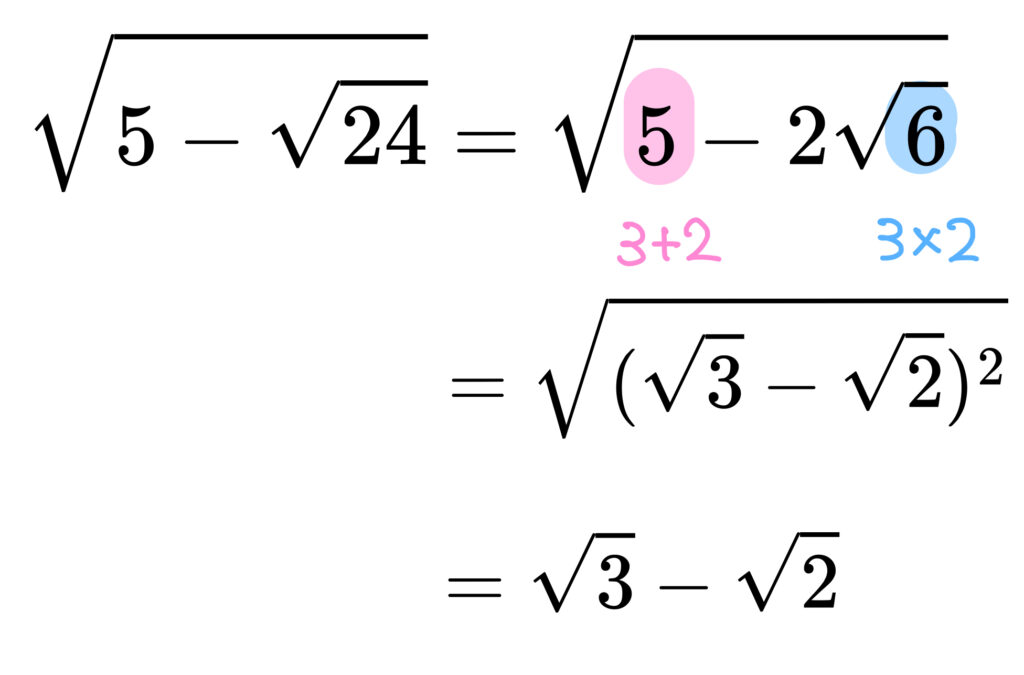
よくできました。ここでやった事を基本に練習を重ねてみて下さい。
\(\sqrt{a+b\pm2\sqrt{ab}}\) の形の2重根号を外すときは,
\(\sqrt{a+b\pm2\sqrt{ab}}=\left(\sqrt{a}\pm\sqrt{b}\right)^2=|\sqrt{a}\pm\sqrt{b}|\)
絶対値については以下のページで紹介しています。
絶対値の扱い




コメント