先生!放物線 \(y=ax^2\) を\(x\)軸方向に\(p\) , \(y\)軸方向に\(q\)
だけ平行移動した放物線が \(y=a(x-p)^2+q\)
と教科書に書いてあったのですが、、よくわかりません。
たしかに、1回見ただけではよくわかりませんよね。
まずは以下を見てください。
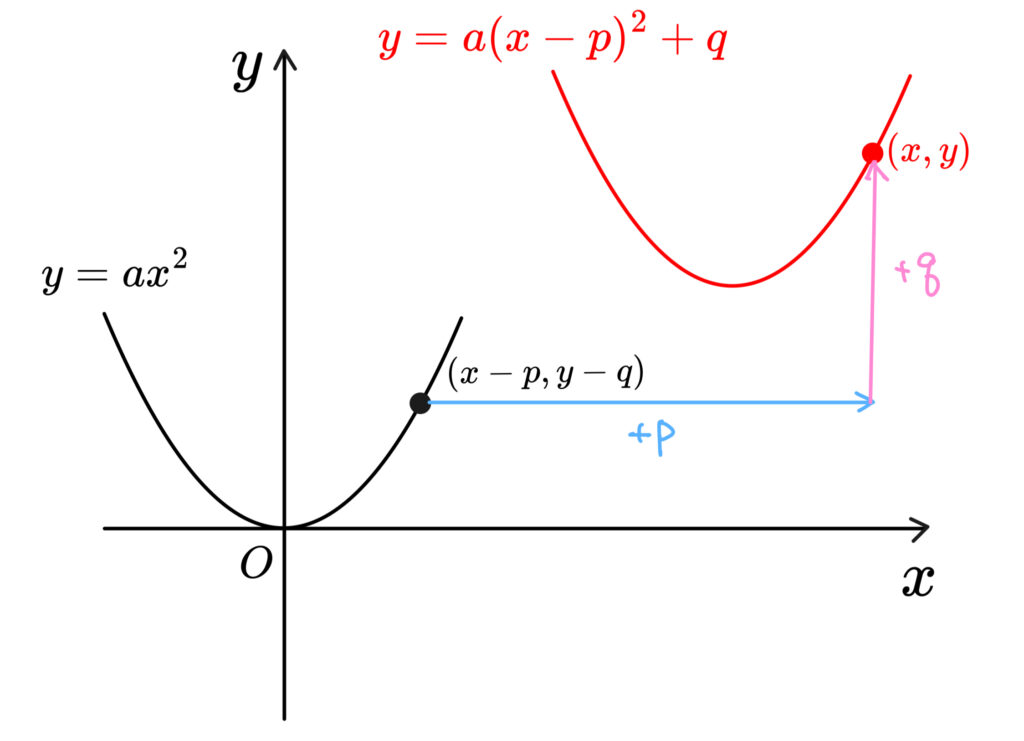
こういうことですか?
\(y=ax^2\) を\(x\)軸方向に\(p\) , \(y\)軸方向に\(q\)
だけ平行移動した放物線上の点 \((x,y)\) は
\({p,q}\) だけ戻せば \(y=ax^2\) に乗っかる点!
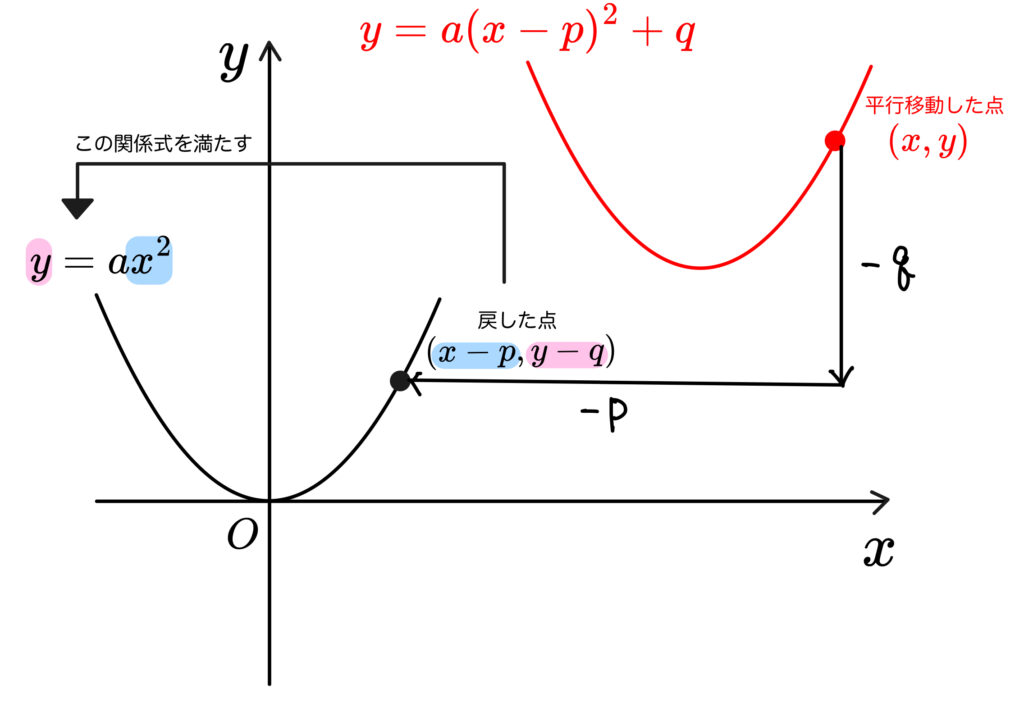
移動前の点は\((x-p,y-q)\) で、
この点が \(y=ax^2\) の関係式を満たしているから、
\(y-q=a(x-p)^2\)
移項すれば \(y=a(x-p)^2+q\) になりますね。
そうです!
慣れないうちはピンとこないかもしれませんが、
グラフを移動する際にとても重要な考え方です。
ありがとうございます。
これで2次関数の軸と頂点の話も理解できそうです!
ちなみに一般の関数について以下のことが言えます。
\(y=f(x)\) の平行移動
関数\(y=f(x)\) を \(x\) 軸方向に \(p\) , \(y\) 軸方向に \(q\) だけ平行移動した関数は
\(y-q=f(x-p)\) という式で与えられる。
2次関数だけでなく,一般の関数について言えることなんですね~。
いろんなところで使う場面がありそうですね!




コメント