先生!絶対つきの方程式・不等式の基本はわかりました!
それで今回は応用編ですね?何をやるんですか?
基本編では、\(|x+1|<2\) のように右辺が定数でした。
今回は \(|x+1|<x\) のように右辺に変数の場合を扱います。
なるほど、右辺に文字が入ってくるんですね…。
どうやって解くんでしょう?
基本は場合分けをして絶対値を外すことを心がけましょう。
まずは問題です。
\((1)~~|x-3|=2x\) を解け。 \((2)~~|2x-4|<x+1\) を解け。
とりあえず、\((1)\) の左辺だけ外してみます。
\begin{eqnarray}
|x-3|
=
\begin{cases}
x-3 & (x\geqq 3 ) \\
-(x-3) & ( x < 3 )
\end{cases}
\end{eqnarray}
お、いいですね~。
ではそれぞれの場合の方程式を解いてみましょう。
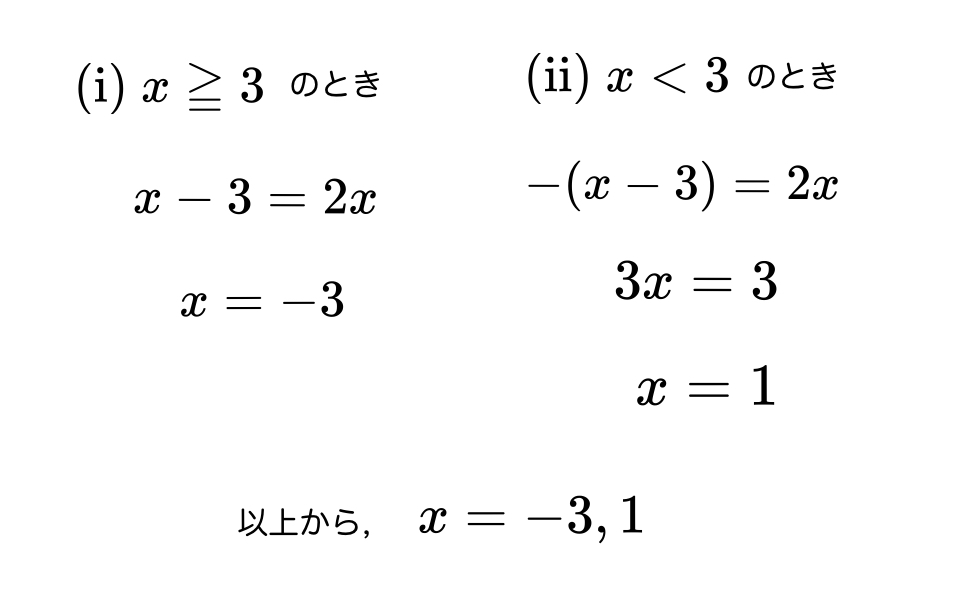
ふぅ~。出来た!
答えは \(x=-3~,~1\)
残念!
よくある間違いなんですが、以下を確認してください。

そっか…。
ちゃんと場合分けした範囲を確認しなきゃいけないんですね。
じゃあ答えは \(x=1\) のみですか?
それで正解です!
ただ確認作業ってついつい忘れてしまいがちなんですよね。
そこでグラフを書いて目で確認してみましょう!
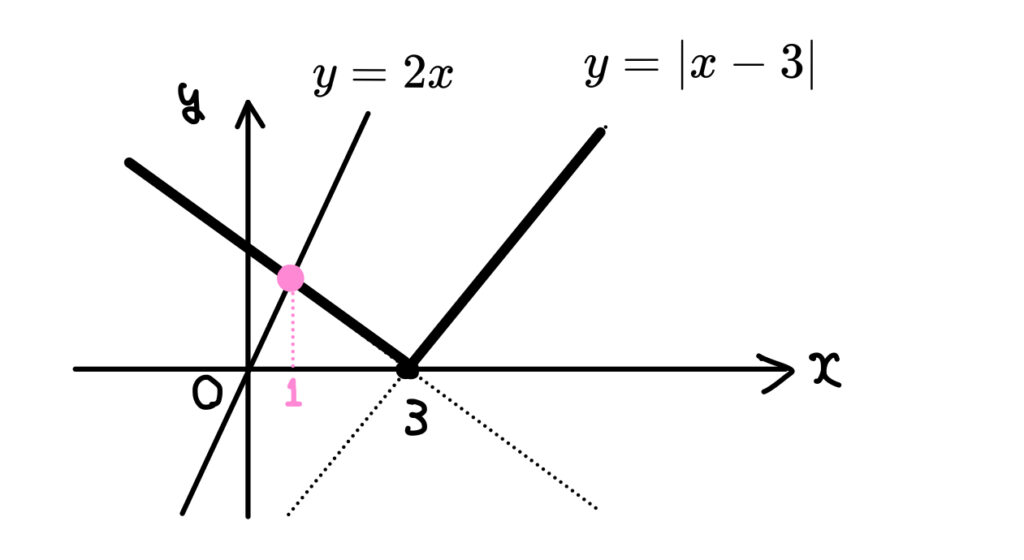
こう見ると、場合分けされている実感がわきますね。
じゃあ \((2)\) もやってみます!まずは場合分けっと…。
\begin{eqnarray}
|2x-4|
=
\begin{cases}
2x-4 & (x\geqq 2 ) \\
-(2x-4) & ( x < 2 )
\end{cases}
\end{eqnarray}
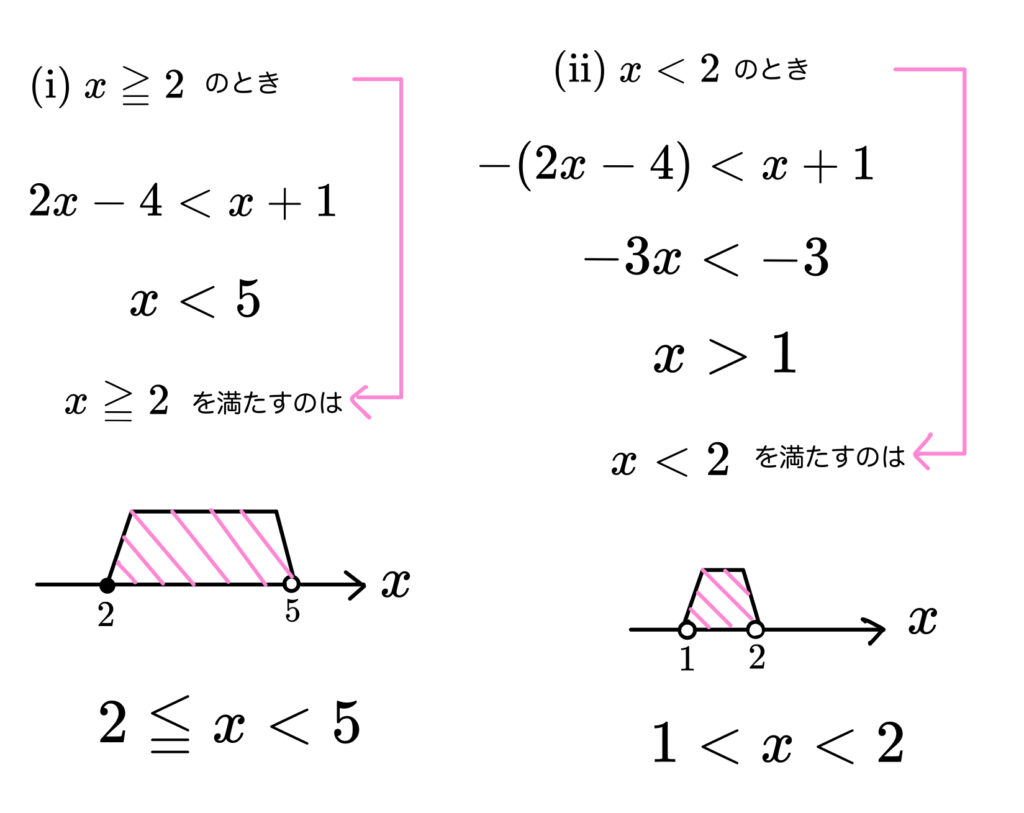
n浪君。いい感じですね。
ただ、もう少し解答をまとめておくといいかもしれません。
えーと…。
あっ、2がつながるから \(1<x<5\) としていいのか。
そうですね。
最後にもう一度、グラフを書いて目で確かめましょう。
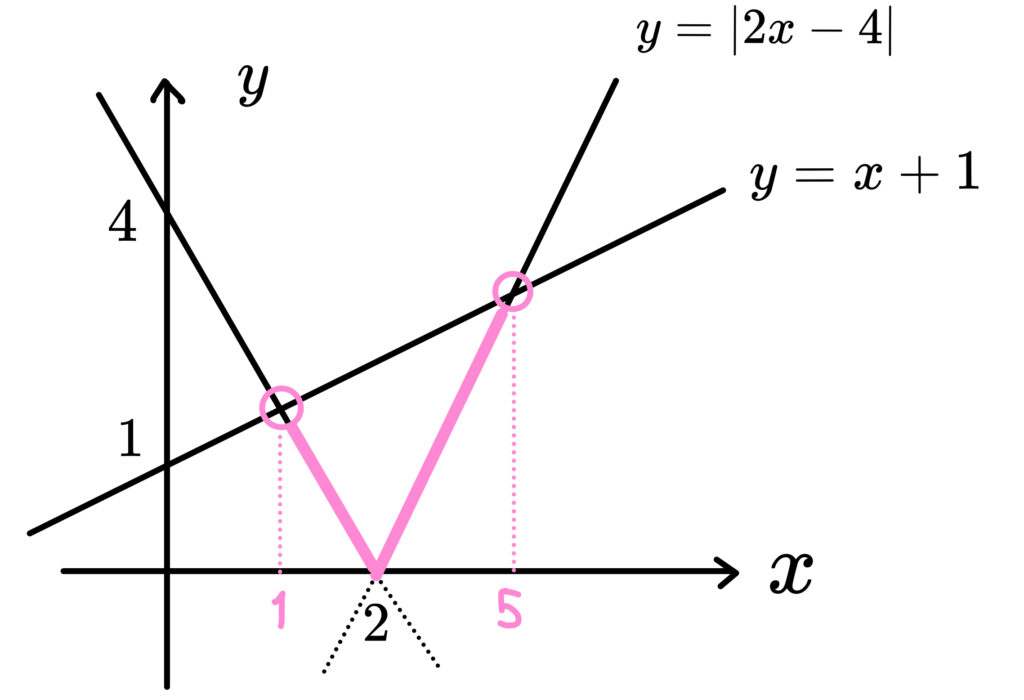
\(y=x+1\) よりも \(y=|2x-4|\) が小さい部分に色を塗ったんですね!
これで \(1<x<5\) が出てくる理由がわかりました。
先生、ありがとうございます!
絶対値の基本的な扱いはコチラ 絶対値の扱い




コメント