先生!2次関数の平行移動は理解できたので、
今日は2次関数の軸と頂点について学習したいです!
n浪君。意欲的ですね。
では最初に \(y=ax^2\) の軸と頂点は答えられますか??
はい!これでどうでしょう?
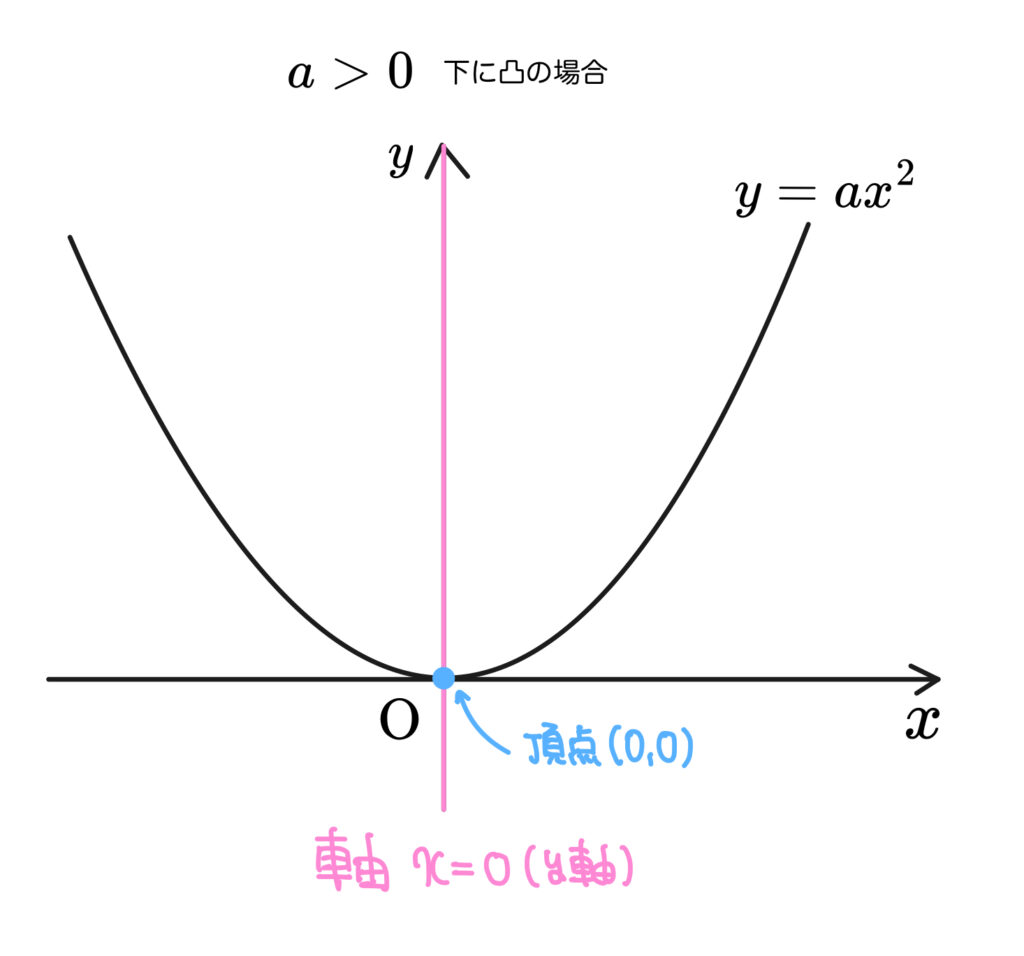
OKです。
それでは \(y=a(x-p)^2+q\) の軸と頂点についてまとめましょう。
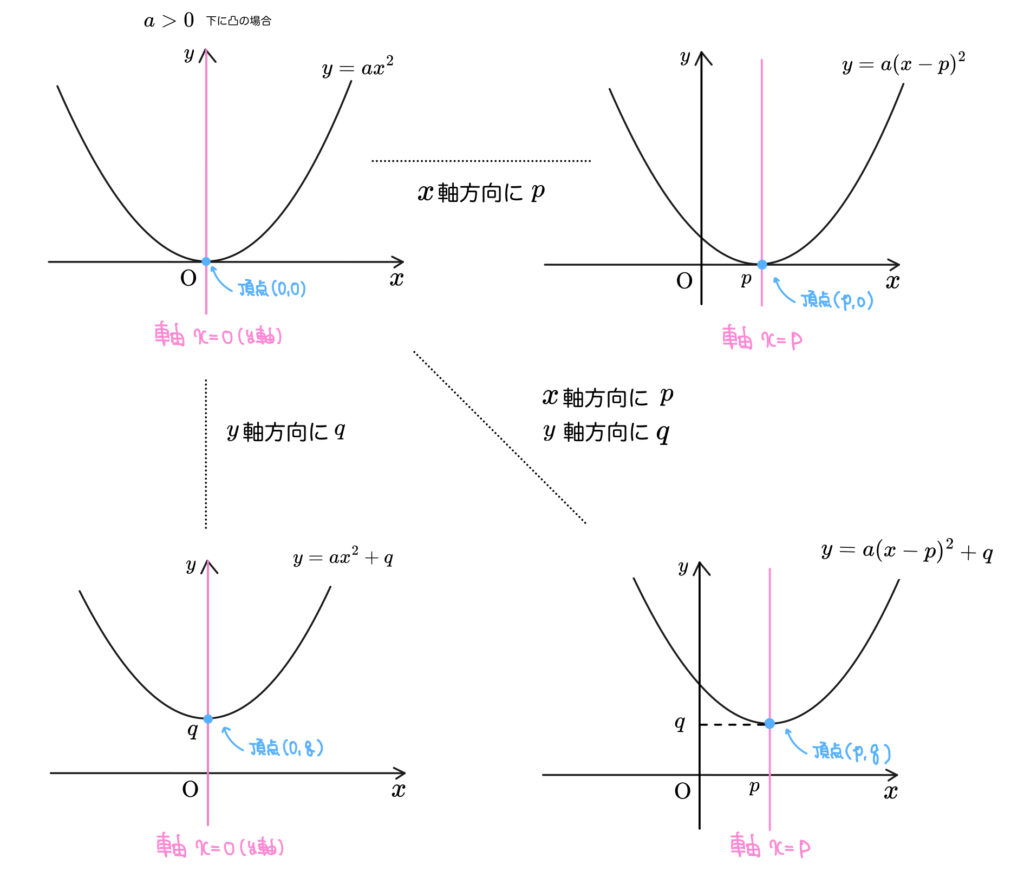
なるほど。
いくつか問題をやって確認してみます。
では以下の2つの2次関数の軸と頂点を求めてみましょう。
問題
以下の2次関数の軸と頂点を求めよ。
\((1)~~y=-(x-3)^2+5\)
\((2)~~y=2x^2+4x-7\)
\((1)~\)は式を見ればすぐわかります!
答えは軸:\(x=3\),頂点:\((3,5)\) ですね。
正解です。では\((2)~\)はいかがでしょう?
\((2)~\)は平方完成して\(y=a(x-p)^2+q\) の形に変形する必要がありますね。
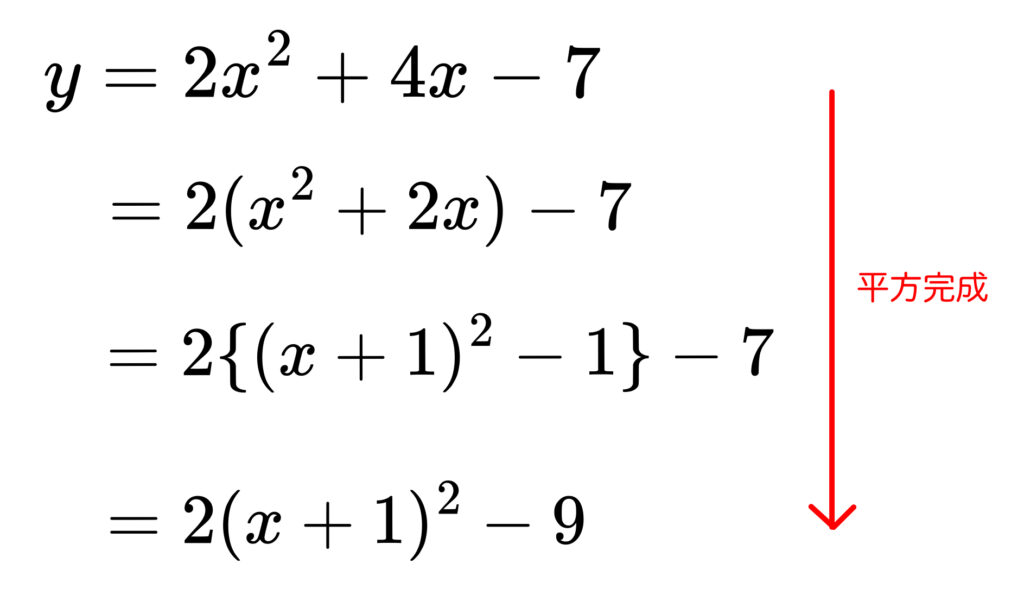
うまくできました。
つまり答えは軸:\(x=-1\),頂点:\((-1,-9)\) です!
素晴らしい!
計算もばっちりですね。




コメント