
立体のイメージがわかないので,とりあえず断面を考察しよう。
x,yについての対称性を崩さないように, 平面 \(z=t\) で切る誘導がついている。

あとはtを0から1まで動かして積分しましょう。
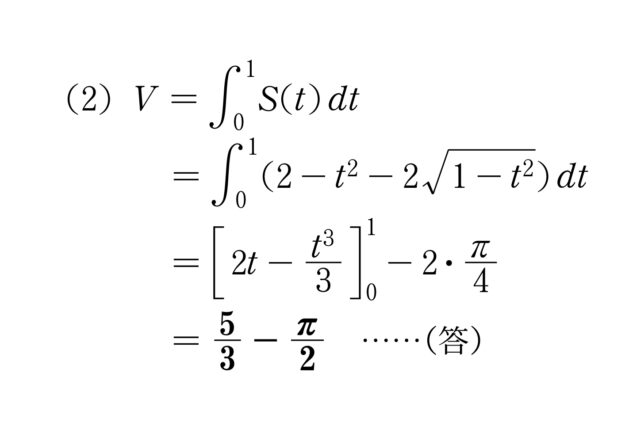
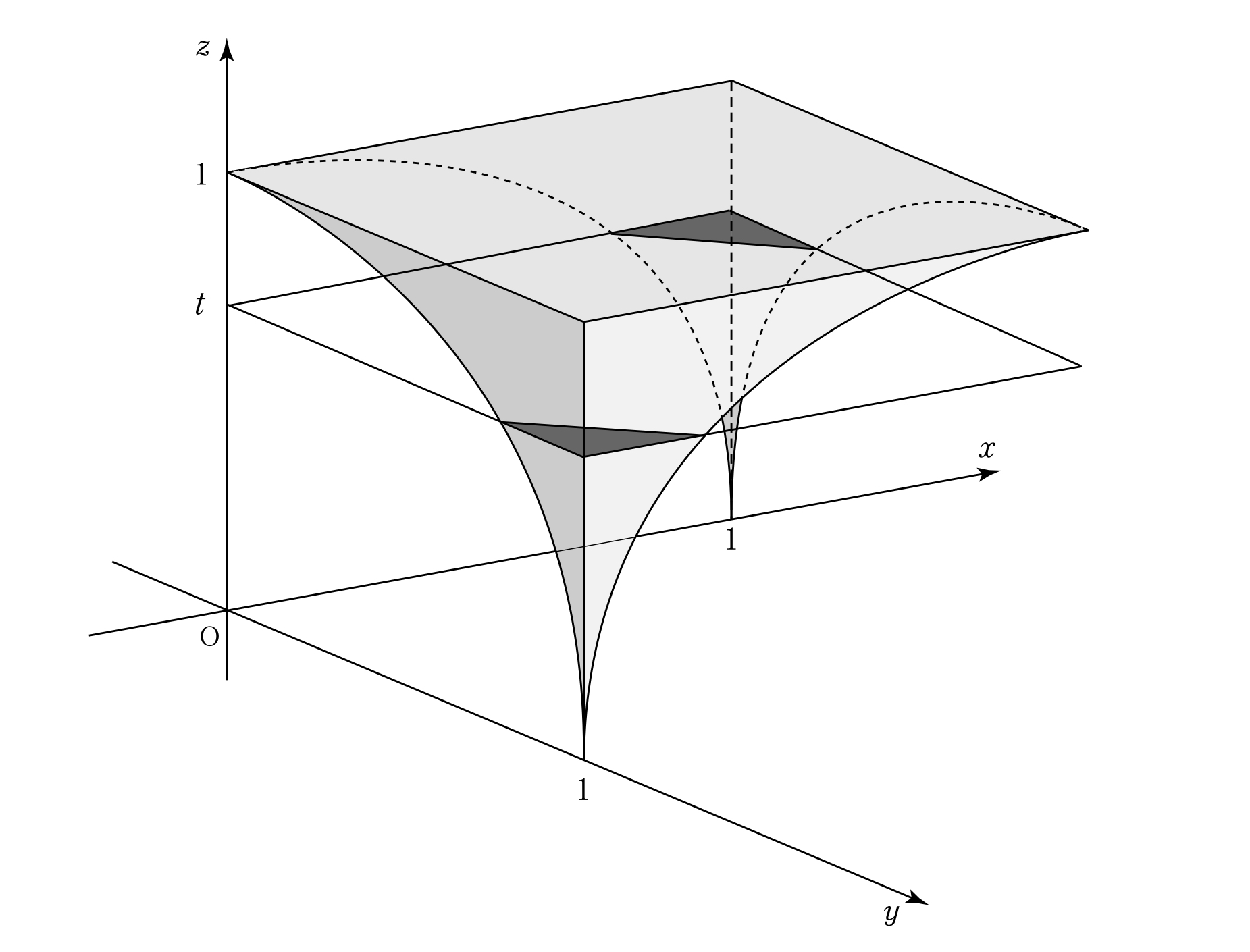
$xyz$空間において,次の連立不等式が表す立体を考える。
0\leqq{x}\leqq{1},0\leqq{y}\leqq{1},0\leqq{z}\leqq{1},x^2+y^2+z^2-2xy-1\geqq{0}
(1)この立体を平面$z=t$で切ったときの断面を$xy$平面に図示し,この断面の面積$S(t)$を求めよ。\ (2)この立体の体積$V$を求めよ。【北海道大学2007年】
(1)題の連立不等式が表す立体を$(\ast)$と名づける。\ $(\ast)$を平面$z=t\,(0\leqq{t}\leqq{1})$ で切ったときの断面の領域は\ ~$\trenritu{0\leqq{x}\leqq{1}\0\leqq{y}\leqq{1}\x^2+y^2+t^2-2xy-1\geqq{0}}$\
$\douti$
$\trenritu{0\leqq{x}\leqq{1}\0\leqq{y}\leqq{1}\(y-x)^2\geqq{1-t^2}}$\
$\douti$
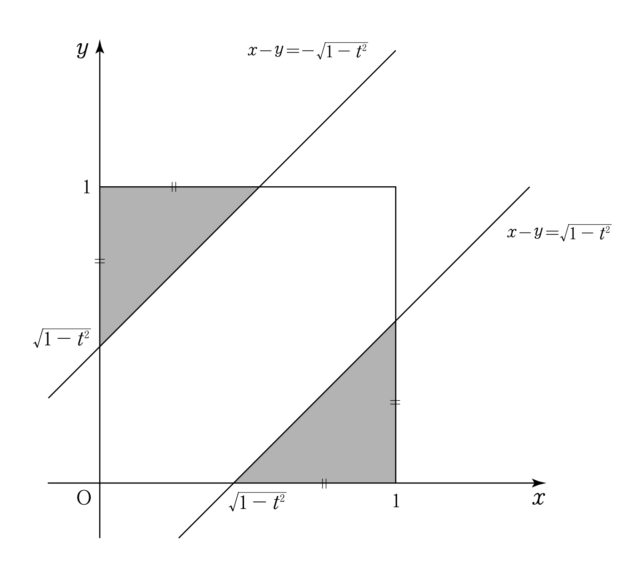
$\trenritu{0\leqq{x}\leqq{1}\0\leqq{y}\leqq{1}\x-y\geqq{\sqrt{1-t^2}},x-y\leqq{-\sqrt{1-t^2}}}$
上の不等式が表す領域を$xy$平面に図示すると右図の色つき部分(境界線含む)。
この色つき部分は1辺の長さが$1-\sqrt{1-t^2}$の2つの合同な直角二等辺三角形
であり,$\bd{S(t)=\left(1-\sqrt{1-t^2}\right)^2}\kotae$\\
(2)~~$V=\dint{0}{1}S(t)\,dt$\
$=\dint{0}{1}(2-t^2-2\sqrt{1-t^2})\,dt$\
$=\teisekibun{2t-\bunsuu{t^3}3}{0}{1}-2\cdot\bunsuu{\pi}{4}$\
$=\bd{\bunsuu53-\bunsuu\pi2}\kotae$




コメント