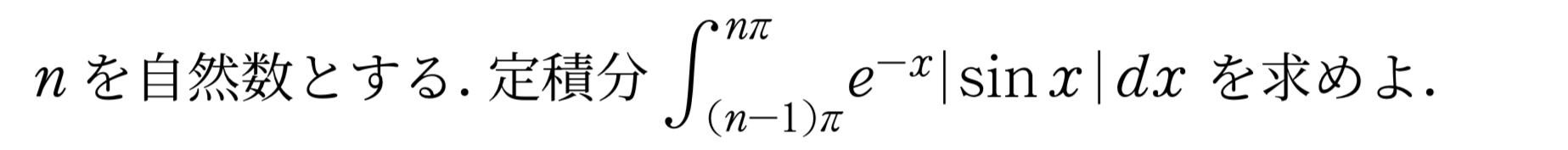
単純に計算するのは大変そうですね。特に絶対値の扱いに困るところです。
この積分計算は少し図形的なイメージを持つことが解答のポイントになります。
\(y=e^{-x} \sin x\) は「減衰曲線」として有名な曲線です。
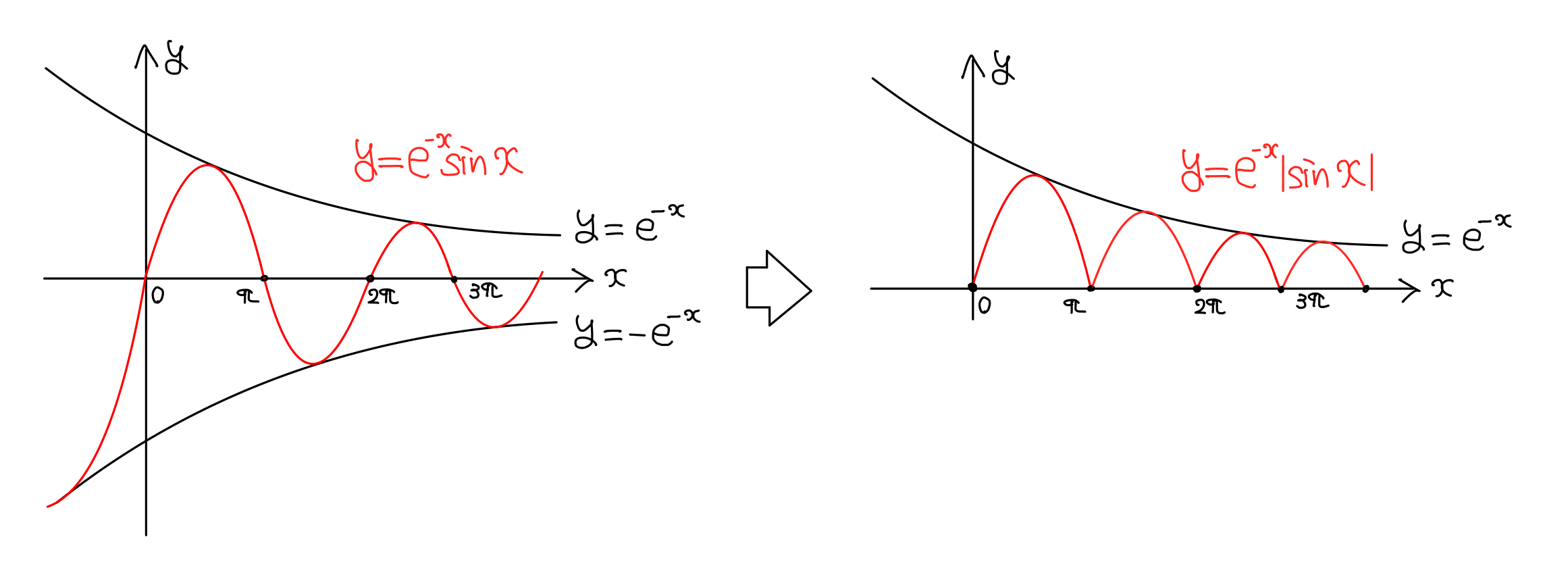
なるほど。\([(n-1)\pi,n\pi]\) の区間で積分するとなると
\([(偶数)\pi,(奇数)\pi]\) では,\(\sin x\geq 0\)
\([(奇数)\pi,(偶数)\pi]\) では,\(\sin x\leq 0\)
なので自然数\(n\) を偶奇で場合分けすれば計算できそうです。
ですが,場合分けをしなくても計算できる方法を紹介しましょう。
\(t=x-(n-1)\pi\) という置き換えをすることで,区間が\([0,\pi]\)にスライドします。
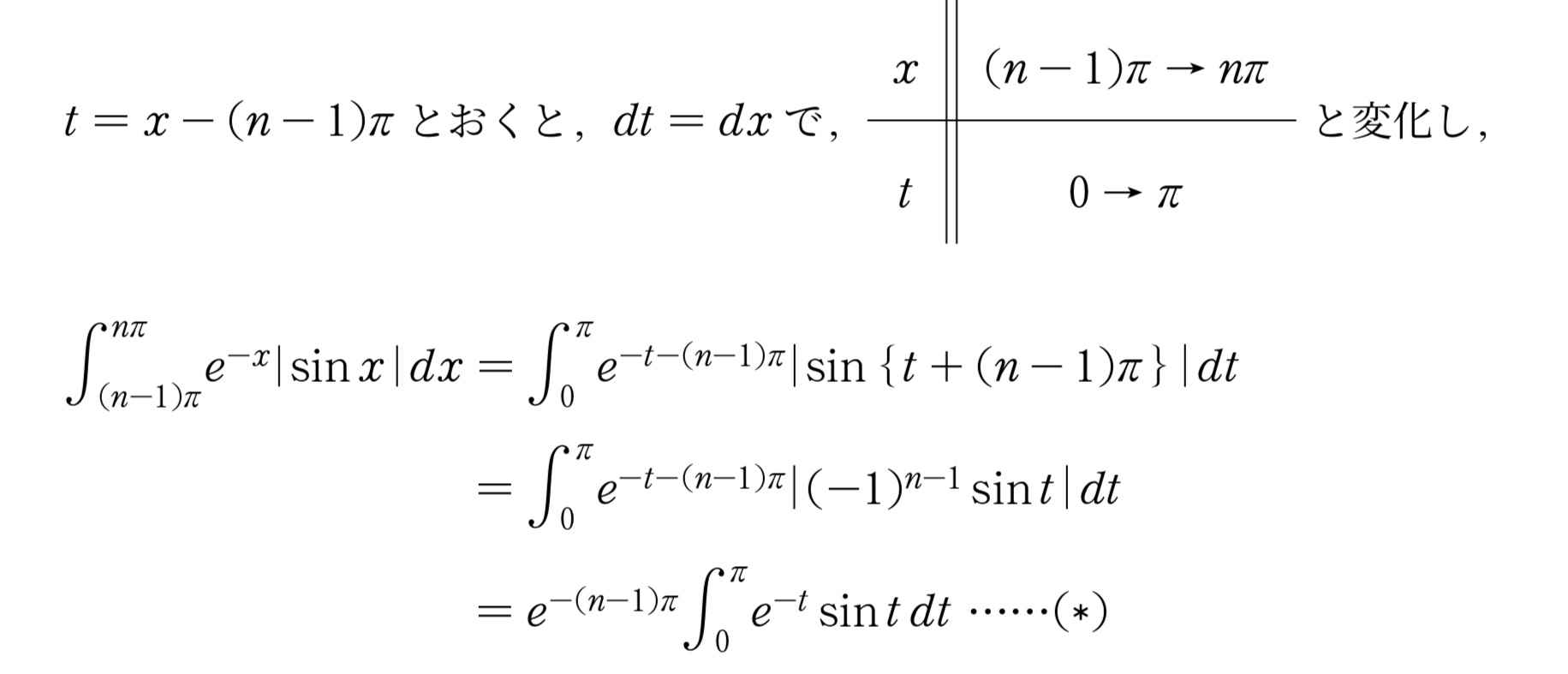
途中計算で,\(\sin (\theta+m\pi)=(-1)^m\sin\theta \) という処理がありました。
さて,あとは定積分\(\displaystyle\int^{\pi}_{0}e^{-t}\sin t dt\) の計算だけ終わらせましょう。
これはいわゆる「同形出現」ってやつですね。
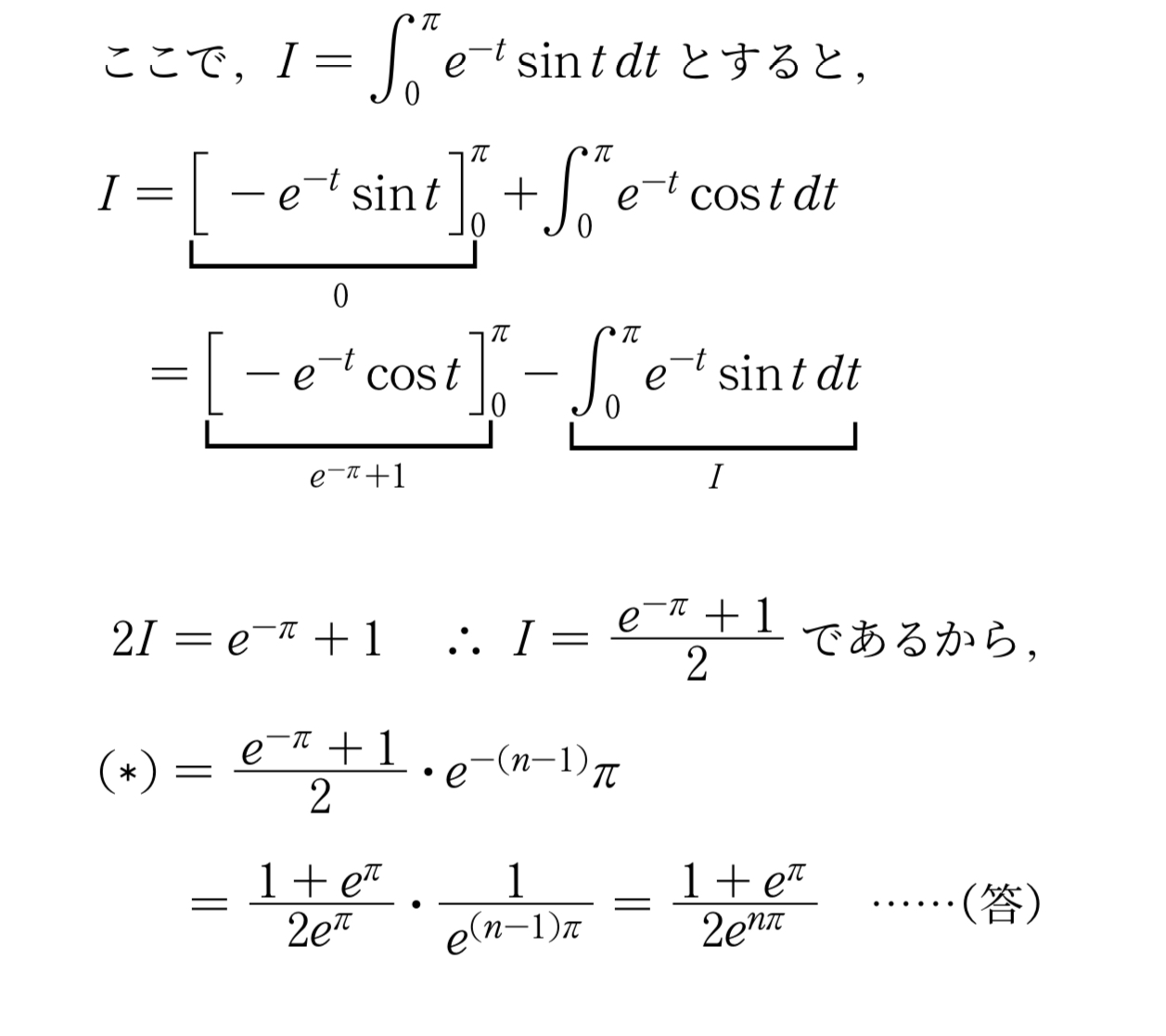
いかがでしたでしょうか。この処理の仕方は何回か練習しておくとよいでしょう。
結論,この問題は初項 \(I\) ,公比 \(e^{-\pi}\) の等比数列の 第 \(n\) 項を求めたことになります。
この事実を理解しておくと,より簡単に答えが確認できるので是非考えてみてください。
$n$を自然数とする.定積分$\dint{(n-1)\pi}{n\pi}e^{-x}\zettaiti{\sin{{x}
}}\,dx$~を求めよ.\
$t=x-(n-1)\pi$とおくと,$dt=dx$で,\begin{tabular}{c||c}
$x$&$(n-1)\pi\to{n\pi}$\\hline
$t$&$0\to\pi$
\end{tabular}~と変化し,\\
$\dint{(n-1)\pi}{n\pi}e^{-x}\zettaiti{\sin{{x}
}}\,dx=\dint{0}{\pi}e^{-t-(n-1)\pi}\zettaiti{\sin\B{t+(n-1)\pi}}\,dt$\
$=\dint{0}{\pi}e^{-t-(n-1)\pi}\zettaiti{(-1)^{n-1}\sin{t}}\,dt$\
$=e^{-(n-1)\pi}\dint{0}{\pi}e^{-t}\sin{t}\,dt~\cdots\cdots(\ast)$\
ここで,$I=\dint{0}{\pi}e^{-t}\sin{t}\,dt$とすると,\
$I=\underbracket{\teisekibun{-e^{-t}\sin{t}}{0}{\pi}}{0}+\dint{0}{\pi}e^{-t}\cos{t}\,dt$\ $=\underbracket{\teisekibun{-e^{-t}\cos{t}}{0}{\pi}}{e^{-\pi}+1}-\underbracket{\dint{0}{\pi}e^{-t}\sin{t}\,dt}_{I}$\\
~$2I=e^{-\pi}+1$~~~~$\yueni~I=\bunsuu{e^{-\pi}+1}{2}$であるから,\
$(\ast)=\bunsuu{e^{-\pi}+1}{2}\cdot{e^{-(n-1)}\pi}$\
\hspace{7mm}$=\bunsuu{1+e^\pi}{2e^\pi}\cdot\bunsuu{1}{e^{(n-1)\pi}}=\bunsuu{1+e^\pi}{2e^{n\pi}}\kotae$




コメント