
立体のイメージがわかないので,とりあえず平面 \(z=t\) 上でどんな断面なのかを考察してみよう。
\(\overrightarrow{OR}\) は \(\overrightarrow{OP}\) でいったん線分上をのぼって, \(\overrightarrow{OQ}\) でそこから半径1の円周上に移動する。

では \(z=\cos\theta\) 上で断面を考察しよう。
立体の共通部分は「断面の共通部分」を考えるのがポイント
あとは \(z\) について0から1まで積分して終了!

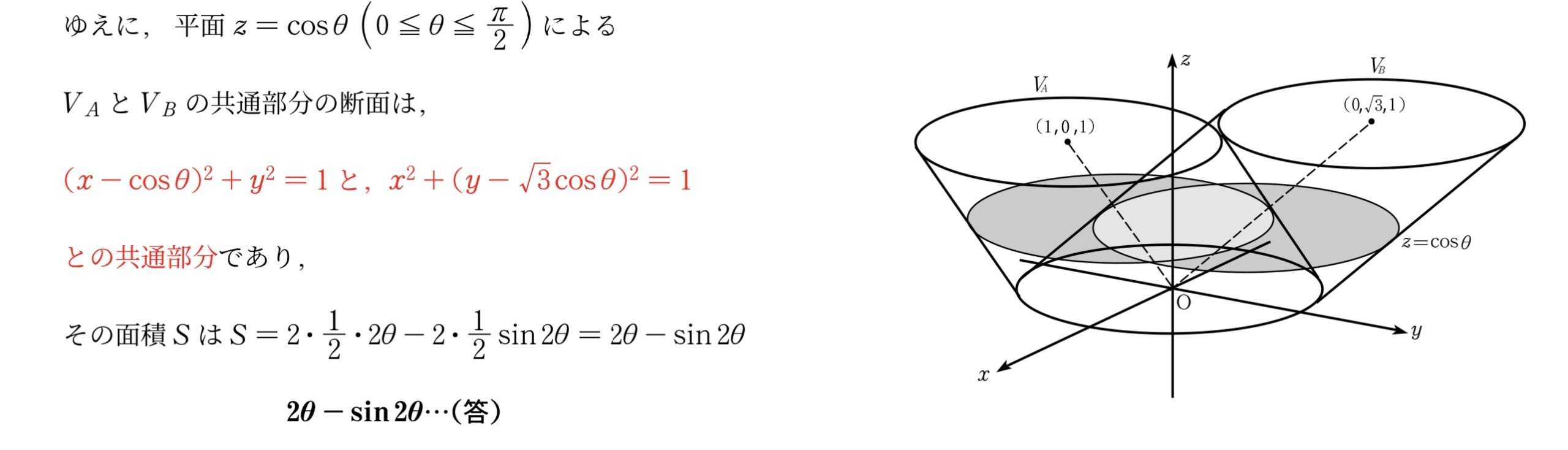
$xyz$空間に3点O($0,0,0$),A($1,0,1$),B($0,\sqrt{3},1$)がある。平面$z=0$に含まれ,中心がO,半径が1の円を$W$とする。点Pが線分OA上を,点Qが円$W$の周および内部を動くとき,$\Vec{OR}=\Vec{OP}+\Vec{OQ}$を満たす点R全体が作る立体を$V_{A}$とおく。同様に点Pが線分OB上を,点Qが円$W$の周および内部を動くとき,$\Vec{OR}=\Vec{OP}+\Vec{OQ}$を満たす点R全体が作る立体を$V_{B}$とおく。更に$V_{A}$と$V_{B}$の重なり合う部分を$V$とする。\
(1)平面$z=\cos\theta~\p{0\leqq{\theta}\leqq\bunsuu\pi2}$による立体$V$の切り口の面積を$\theta$を用いて表せ。\ (2)立体$V$の体積を求めよ。
(1)~~立体$V_A$について,点Rは平面\textcolor{teal}{$z=t$}上で$(t,0,t)$を中心とする半径1の円の周および内部を動く。\
同様に立体$V_B$について,点Rは平面\textcolor{teal}{$z=t$}上で$(0,\sqrt{3}t,t)$を中心とする半径1の円の周および内部を動く。\
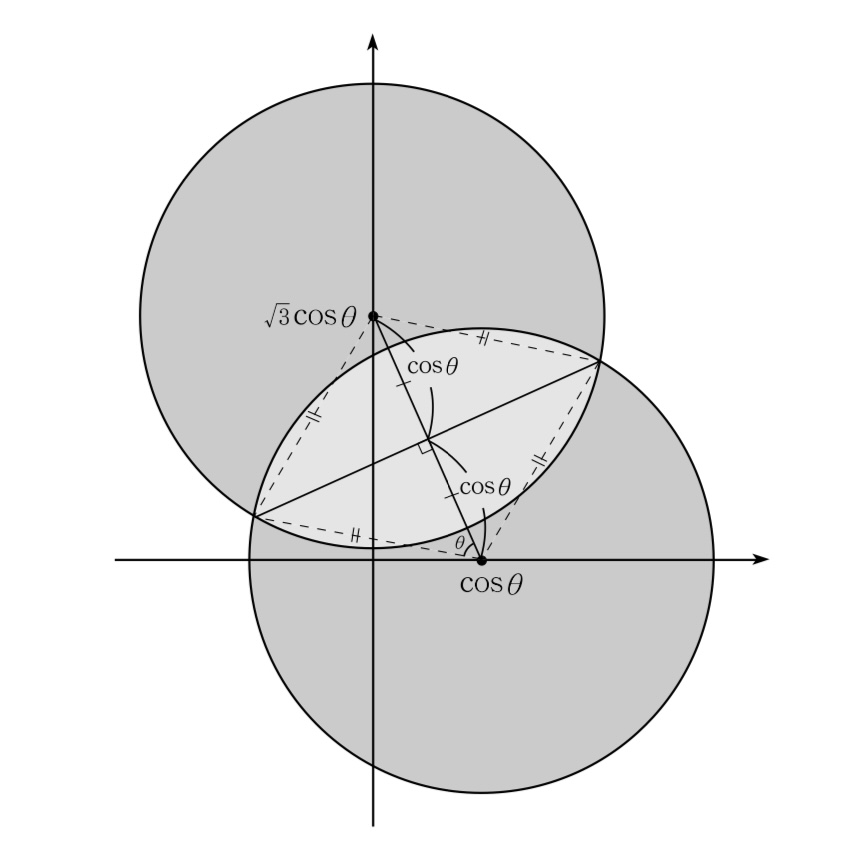
ゆえに,平面$z=\cos\theta~\p{0\leqq{\theta}\leqq\bunsuu\pi2}$による\
$V_A$と$V_B$の共通部分の断面は,\
\textcolor{red}{$(x-\cos\theta)^2+y^2=1$と,$x^2+(y-\sqrt{3}\cos\theta)^2=1$\との共通部分}であり,\
その面積$S$は$S=2\cdot\bunsuu12\cdot{2\theta}-2\cdot\bunsuu12\sin{2\theta}=2\theta-\sin2\theta$\\ymawarikomi{3}{4}{8.5cm}{handai_taiseki2.ai}{8cm}{32}%
(2)~~立体$V$の体積は\\
$\dint{0}{1}S\,dz=\dint{\frac\pi2}{0}(2\theta-\sin2\theta)\cdot(-\sin\theta)d\theta$~\temarkua~\textcolor{blue}{$z=-\cos\theta$}と置換\\
~~~~~~~~~~~$=\dint{0}{\frac\pi2}(2\theta\sin\theta-\sin2\theta\sin\theta)d\theta$\\
~~~~~~~~~~~$=\dint{0}{\frac\pi2}\B{2\theta(-\cos\theta)’-2\sin^2\theta\cos\theta}d\theta$\\
~~~~~~~~~~~$=\p{\teisekibun{-\theta\cos\theta}{0}{\frac\pi2}+\dint{0}{\frac\pi2}\cos\theta\,d\theta-\teisekibun{\bunsuu13\sin^3\theta}{0}{\frac\pi2}}$\\
~~~~~~~~~~~$=2\p{\teisekibun{\sin\theta}{0}{\frac\pi2}-\bunsuu13}=\bunsuu43$\\
$\bd{\bunsuu43\cdots(答)}$




コメント