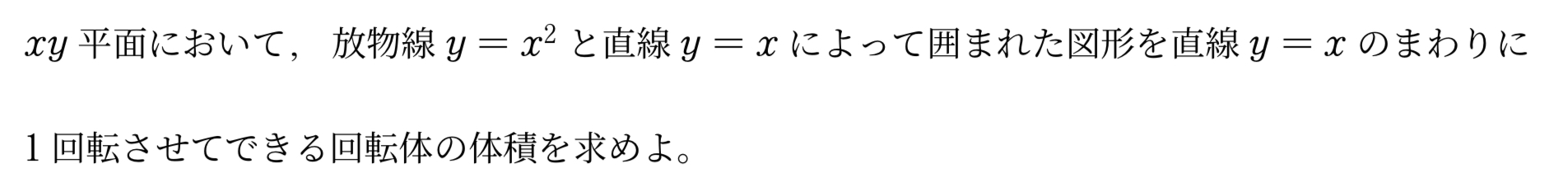
通称「斜軸回転体」です。回転体の体積を求める基本は「回転軸に垂直に切った断面を軸方向に積み上げる」ですので,基本に忠実にやっていきましょう。
とりあえず,軸に垂直な線分\(\rm{PH}\)を考えます。簡単にいえば,\(\rm{PH}\)を半径にもつ円の断面積 \(\pi{\rm PH}^2\) を積み上げていくだけです。
まずは\(\rm{PH}\)の長さを求めていきましょう。

さて,積分する準備は整いました。ですが注意しなければならないのは「\(t\)で積分するわけではない」ということです。積分軸は \(y=x\) なので\(\rm{OH}=s\) などとおいて変数を置き換えます。

ゴール目前ですが,\(|\overrightarrow{\rm PH}|^2\)を \(s\) で表すのは面倒なので,\(t\) で積分しましょう。\(s\) と \(t\) の対応は図で見るとわかりやすいですね。

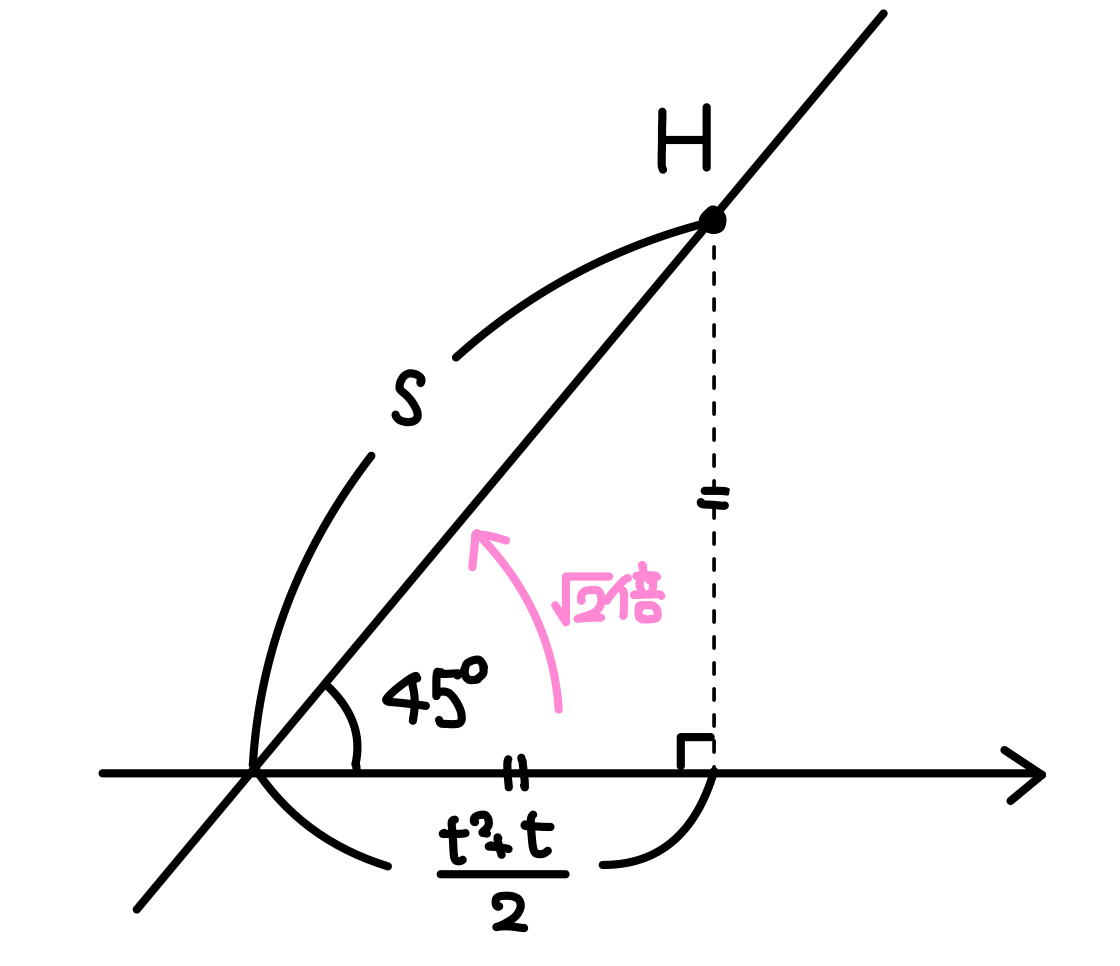
別解として,「カバリエリの原理」を用いた通称:傘型分割による解法を紹介します。
まずは以下の図をご覧ください。

上の図の色つき部分を\(y=x\) の周りに回転させると「傘みたいな立体」が作られます。
この立体の体積はカバリエリの原理によって,結論 「円柱の体積」に近似できます。
カバリエリの原理とは,簡単に言えば「同じ長さの線分を積めば同じ面積」「同じ面積の断面を積めば同じ体積」ということです。
さて,それでは体積を求めていきましょう。

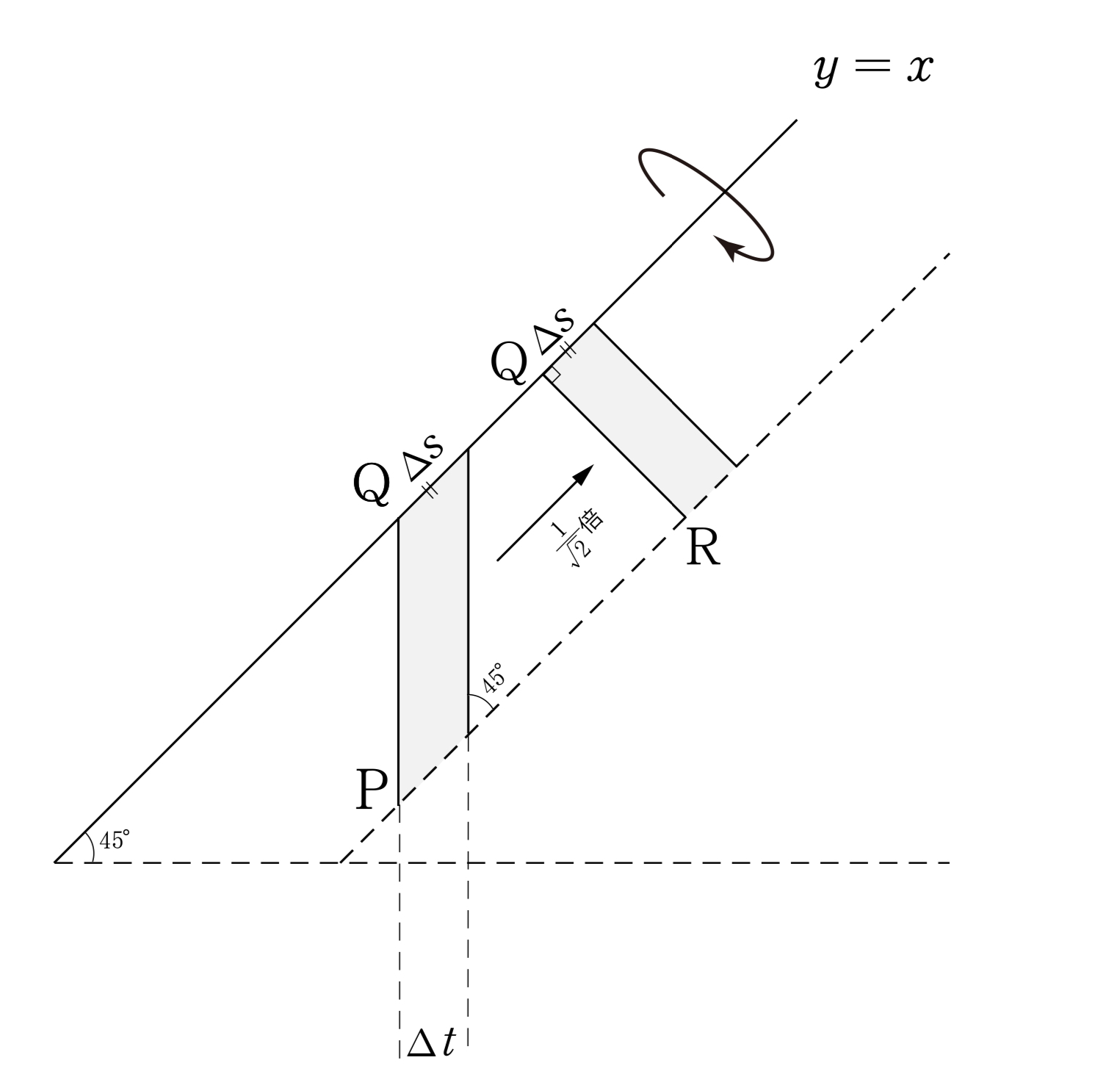
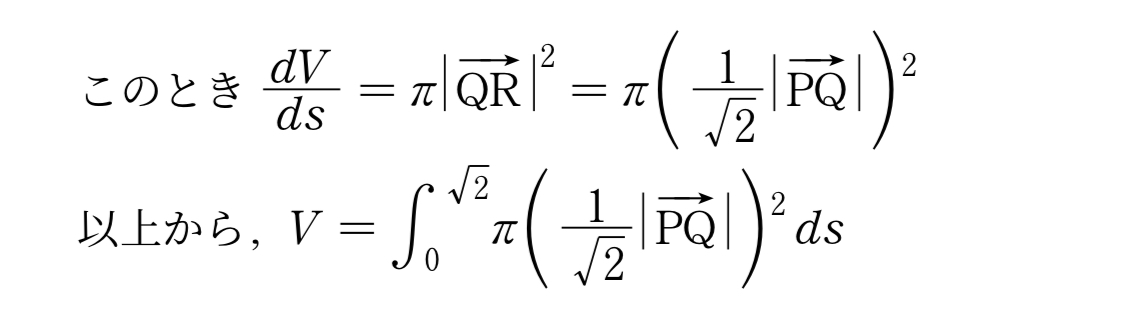
今回の\(s\) と \(t\) の関係はとても簡単で,\(s=\sqrt{2}t\) です。
この\(s,t\) の関係が楽になるのが傘型分割のポイントです。
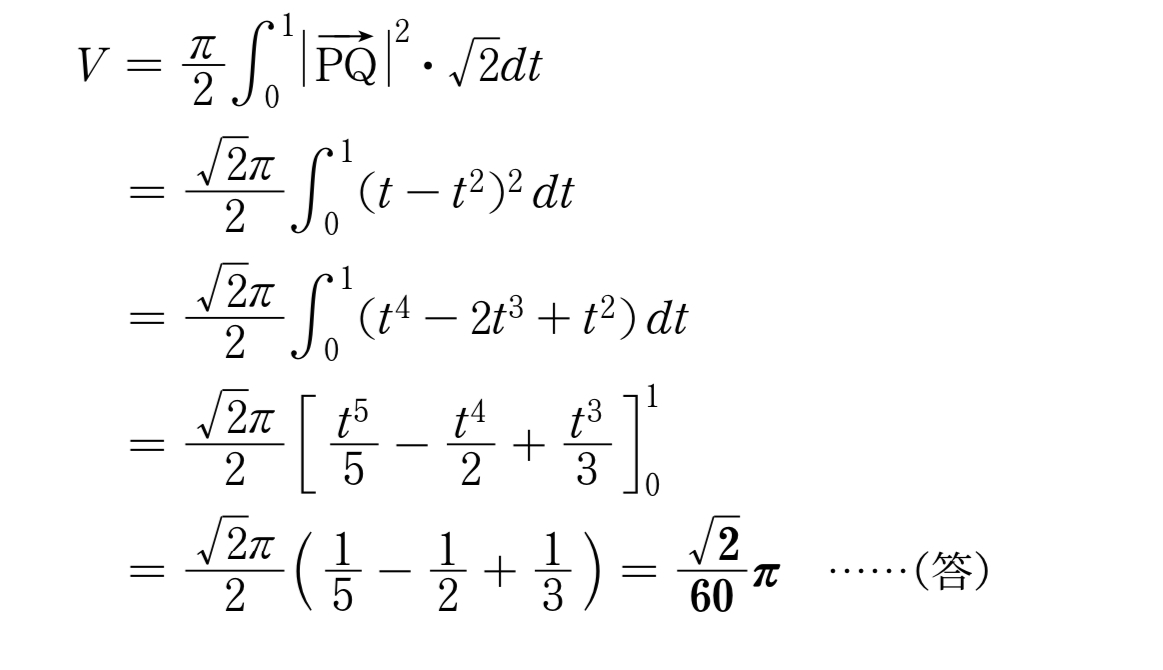
$xy$平面において,放物線$y=x^2$と直線$y=x$によって囲まれた図形を直線$y=x$のまわりに\
1回転させてできる回転体の体積を求めよ。
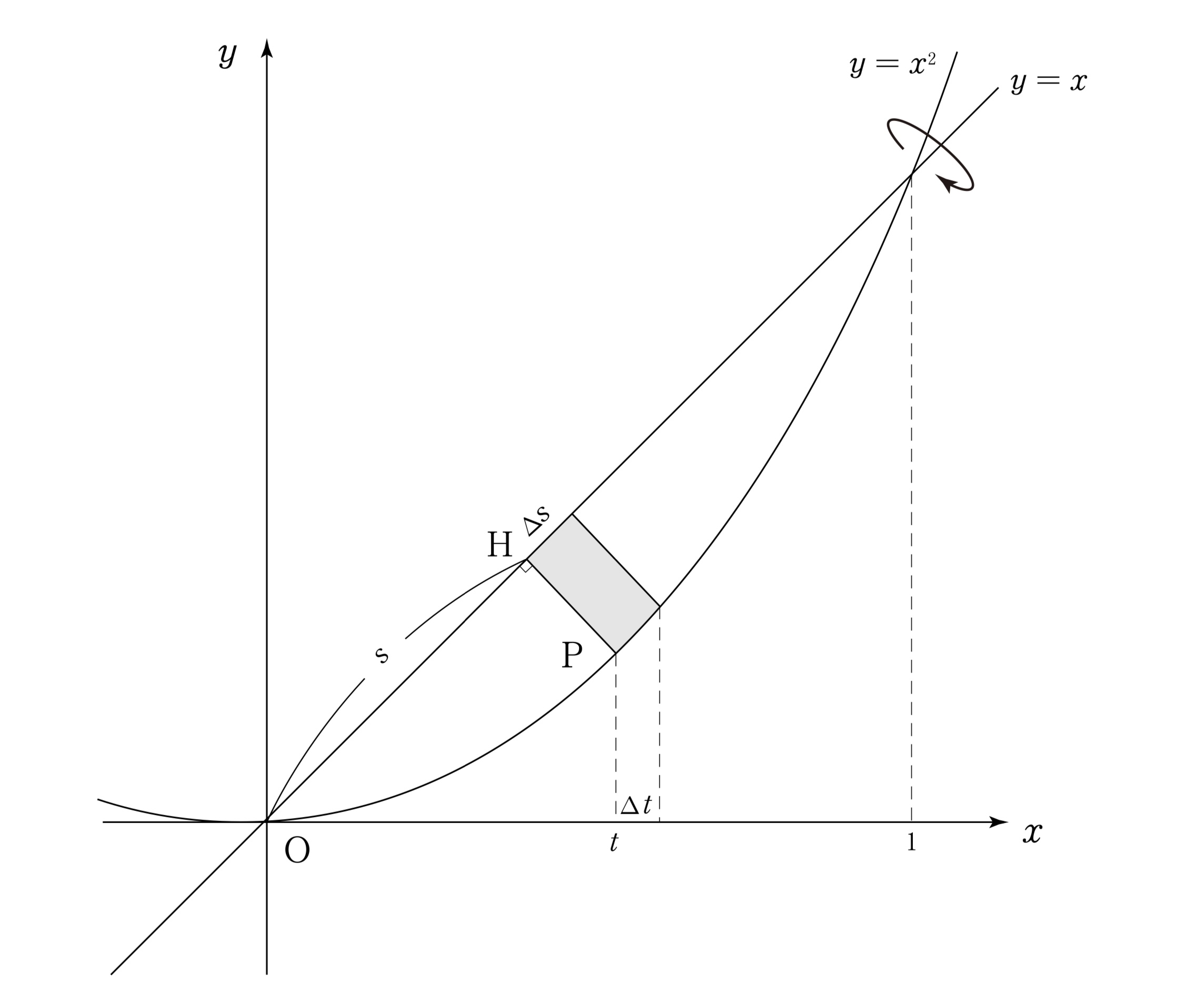
放物線$y=x^2$上に点P($t,t^2$)をとり,点Pから直線$y=x$に下した垂線の足を点Hと定める。\
点Pを通り,$y=x$に垂直な直線は\
\hfill$y-t^2=-(x-t)$\hfill~\
すなわち,\
\hfill$y=-x+t^2+t$\hfill~\
であり,これと$y=x$を連立することで,$x=\bunsuu{t^2+t}{2},y=\bunsuu{t^2+t}{2}$を得る。\
つまり,\
\hfill H$\,\left(\bunsuu{t^2+t}{2},\bunsuu{t^2+t}{2}\right)$\hfill ~\
である。
いま,点Pと点Hの距離$\zettaiti{\Vec{PH}}$は点Pと直線$x-y=0$の距離を考えて,\
\hfill$\zettaiti{\Vec{PH}}=\bunsuu{\zettaiti{t-t^2}}{\sqrt{2}}$\hfill~\
ここでOH$=s$と定めると,\
\hfill$s=\sqrt{2}\cdot\bunsuu{t^2+t}{2}=\bunsuu{t^2+t}{\sqrt{2}}$\hfill~\
以上から,求める回転体の体積を$V$とすると,\
\hfill$V=\dint{0}{\sqrt{2}}\pi\zettaiti{\Vec{PH}}^2\,ds$\hfill~\
である。\
ここで,$s=\bunsuu{t^2+t}{\sqrt{2}}$の置き換えから,$ds=\bunsuu{2t+1}{\sqrt{2}}dt$,\begin{tabular}{c||c}
$s$&0$\to\sqrt{2}$\\hline
$t$&$0\to1$\end{tabular}で,\
$V=\pi\dint{0}{1}\bunsuu{(t-t^2)^2}{2}\cdot\bunsuu{2t+1}{\sqrt{2}}dt$\
$=\bunsuu\pi{2\sqrt{2}}(2t^5-3t^4+t^2)dt$\\
$=\bunsuu\pi{2\sqrt{2}}\teisekibun{\bunsuu{t^6}{3}-\bunsuu35t^5+\bunsuu{t^3}3}{0}{1}$\
$=\bunsuu\pi{2\sqrt{2}}\p{\bunsuu13-\bunsuu35+\bunsuu13}=\bd{\bunsuu{\sqrt{2}}{60}\pi}\kotae$
補足
放物線$y=x^2$上に点P($t,t^2$)をとり,直線$y=x$上に点Q($t,t$)をとる。\
$s$を微小に変化させたときに$y=x^2$と$y=x$で囲まれた図形を$y=x$のまわりに1回転させた\
体積の増分$\bunsuu{dV}{ds}$について考えよう。
このとき$\bunsuu{dV}{ds}=\pi\zettaiti{\Vec{QR}}^2=\pi\p{\bunsuu1{\sqrt{2}}\zettaiti{\Vec{PQ}}}^2$\
以上から,$V=\dint{0}{\sqrt{2}}\pi\p{\bunsuu1{\sqrt{2}}\zettaiti{\Vec{PQ}}}^2\,ds$\\\
$V=\bunsuu\pi2\dint{0}{1}\zettaiti{\Vec{PQ}}^2\cdot\sqrt{2}dt$\
$=\bunsuu{\sqrt{2}\pi}2\dint{0}{1}(t-t^2)^2\,dt$\
$=\bunsuu{\sqrt{2}\pi}2\dint{0}{1}(t^4-2t^3+t^2)\,dt$\
$=\bunsuu{\sqrt{2}\pi}2\teisekibun{\bunsuu{t^5}5-\bunsuu{t^4}2+\bunsuu{t^3}3}{0}{1}$\
$=\bunsuu{\sqrt{2}\pi}2\p{\bunsuu15-\bunsuu12+\bunsuu13}=\bd{\bunsuu{\sqrt{2}}{60}\pi}\kotae$



コメント