問題 ★★☆☆☆
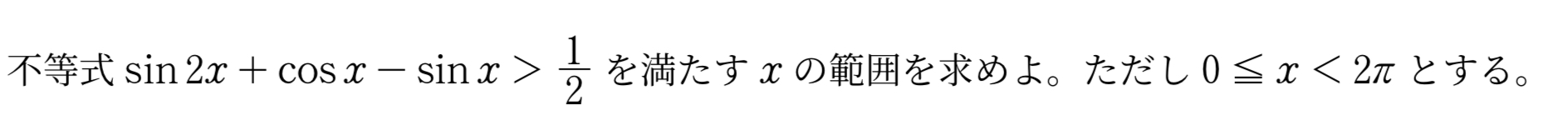
ポイント
\(\sin{x},\cos{x}\) どちらの関数にも統一できないので,
まずは角をそろえて因数分解できないか考えます。
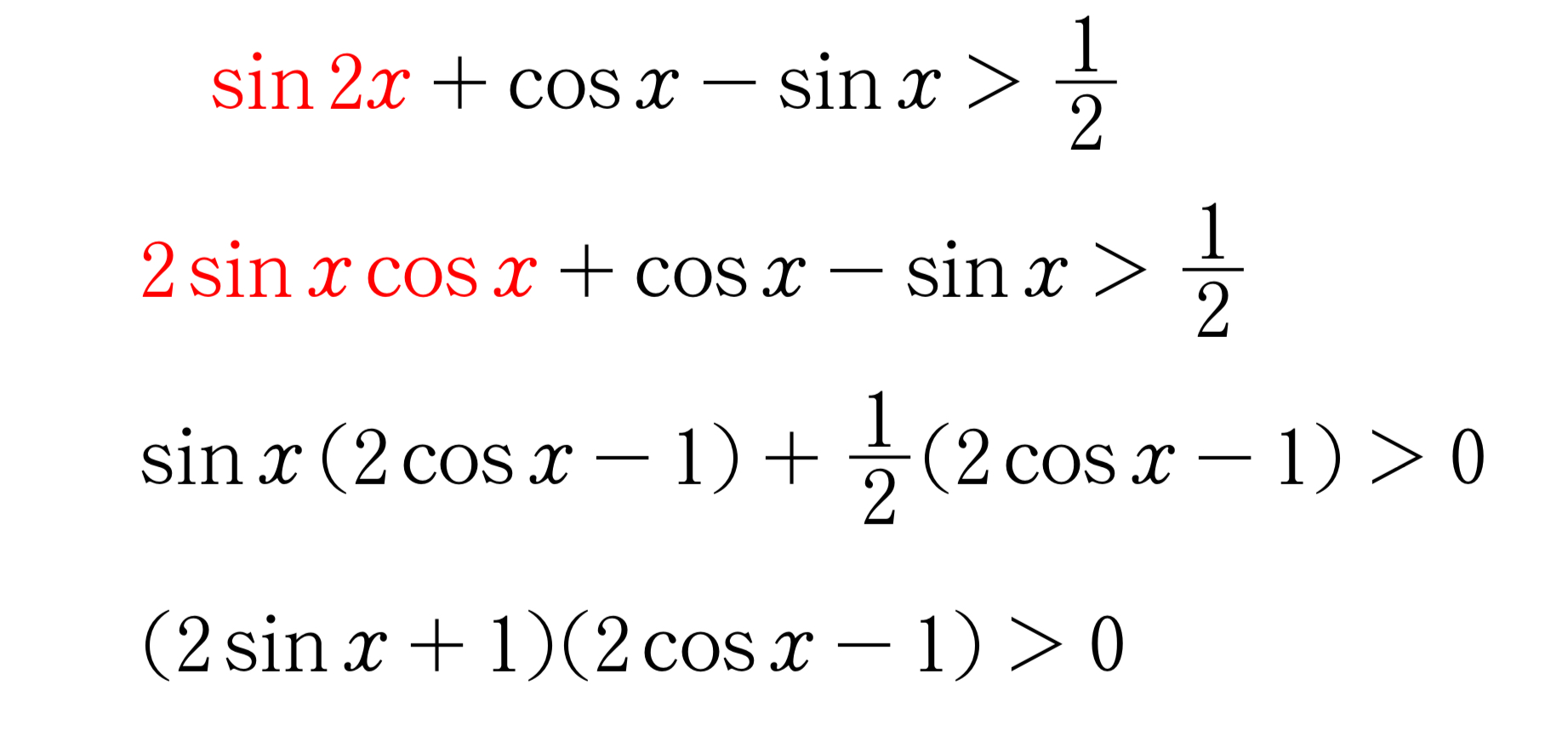
ポイント
因数分解できたので,掛け算がプラスになるような\(\sin{x},\cos{x}\) のとりうる値を考えます。
場合分けしてもよいのですが,単位円周上にそれぞれの因数の符号を書くと早いです。
ポイント
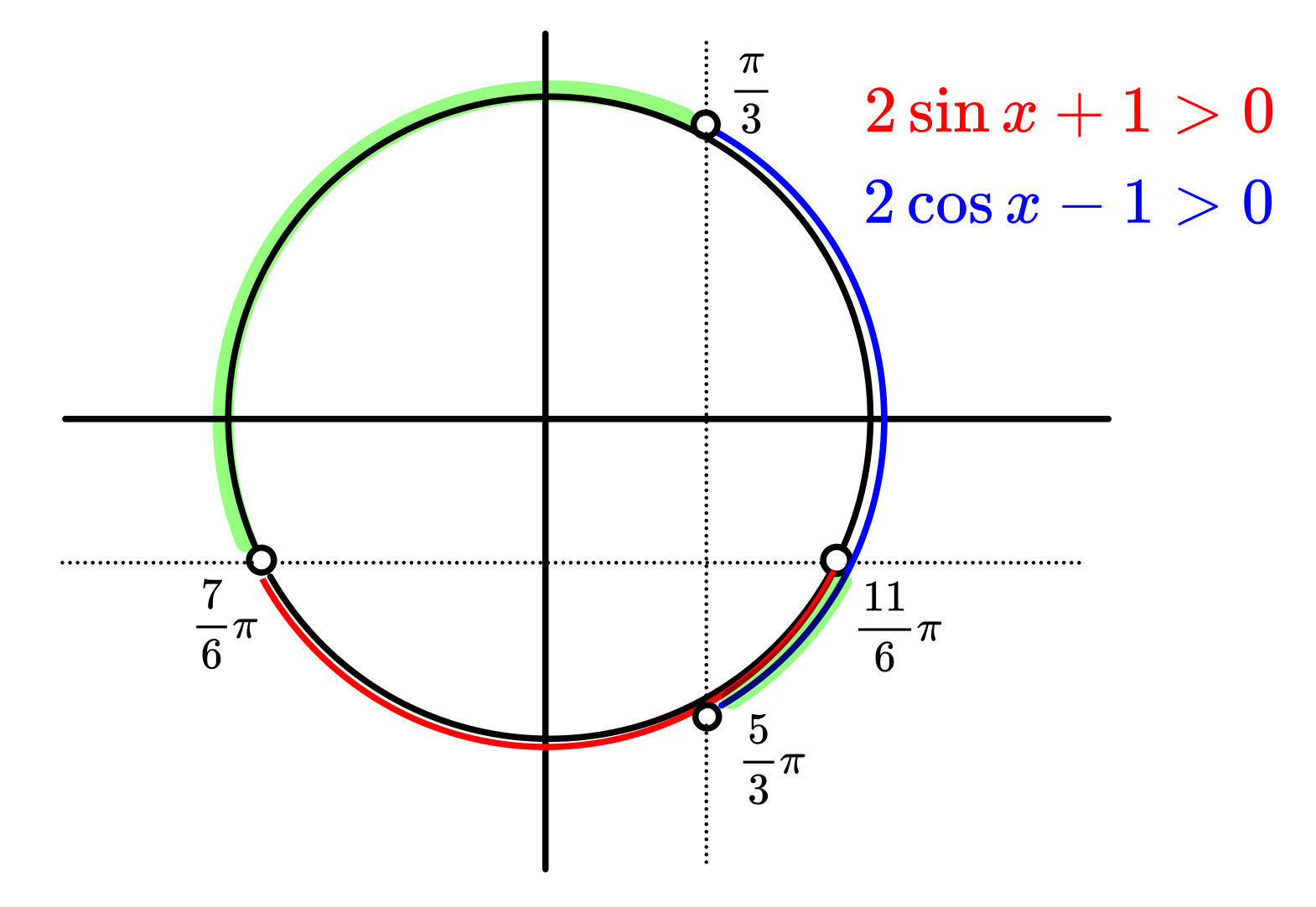
求めるべき\(\theta\) の範囲は上の図における緑のラインです。(どちらも正か,どちらも負のエリア)
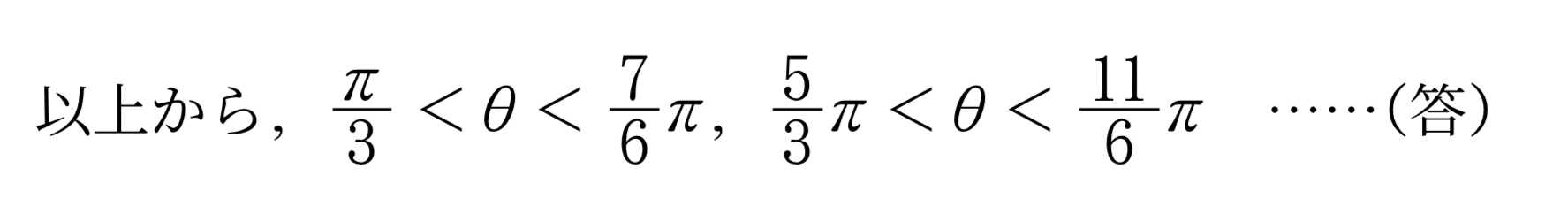
$\sin{2x}+\cos{x}-\sin{x}>\bunsuu12$\
$2\sin{x}\cos{x}+\cos{x}-\sin{x}>\bunsuu12$\
$\sin{x}\,(2\cos{x}-1)+\bunsuu12(2\cos{x}-1)>0$\
$(2\sin{x}+1)(2\cos{x}-1)>0$
以上から,$\bunsuu\pi3<\theta<\bunsuu76\pi$,$\bunsuu53\pi<\theta<\bunsuu{11}6\pi\kotae$




コメント