
立体のイメージはつかめなくてよい。
軸に垂直な平面で切ったときの断面を考える。
このとき,登場回数の多い文字や次数の高い文字が定数になるように平面を選択しよう。

今回の断面は不等式から台形とわかるが,tの値によって図形が変化するので場合分けしよう。
あとはそれぞれの断面積を求めて積分すれば終了ですね。
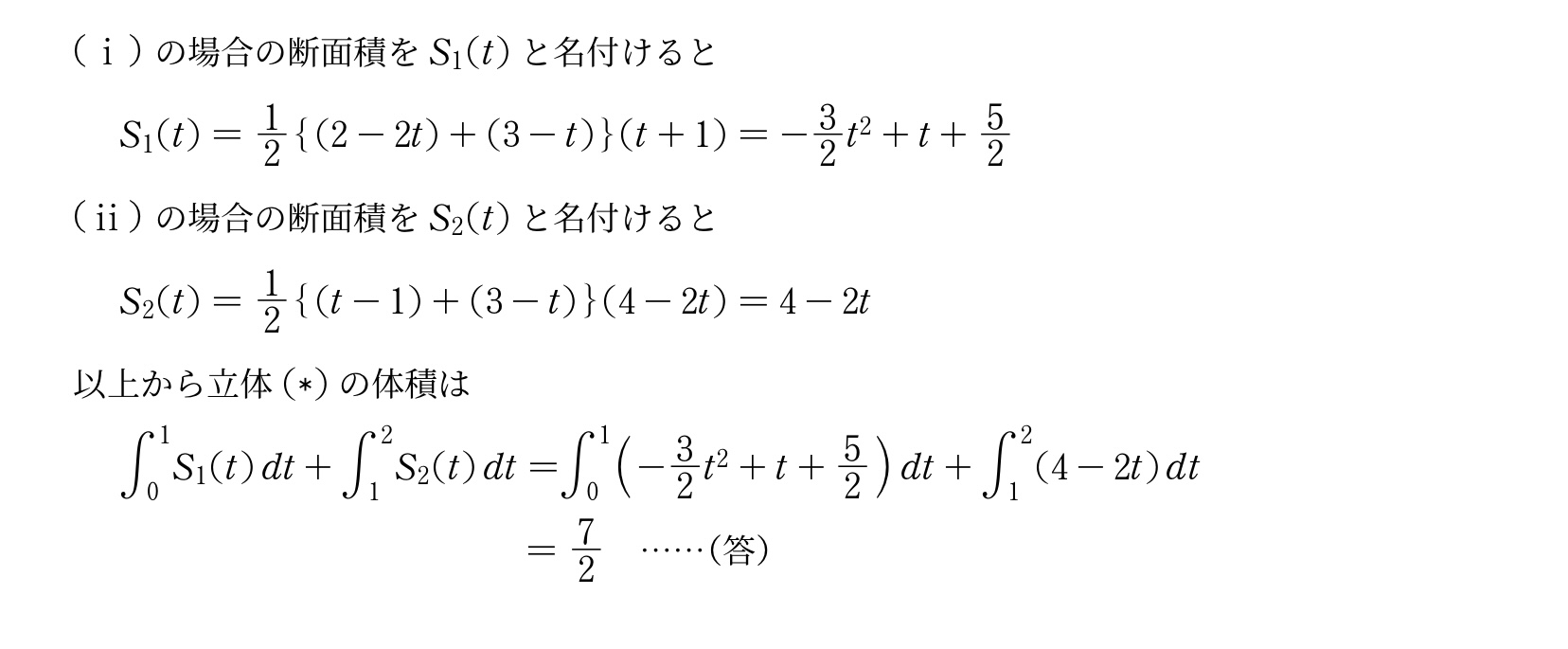
$xyz$空間内において次の6個の不等式で表される立体の体積を求めよ。\
\hfill~$x\geqq{0},~y\geqq{0},~z\geqq{0},~x+y+z\leqq{3},~x+2z\leqq{4},~y-z\leqq{1}$【1988年~東大~文科】
連立不等式$x\geqq{0},~y\geqq0,~z\geqq0,~x+y+z\leqq{3},~x+2z\leqq4,~y-z\leqq1$\
で表された立体を$(\ast)$と名付ける。\
平面$z=t~(t\geqq{0})$による$(\ast)$の断面は,連立不等式\
$x\geqq{0},~y\geqq0,~t\geqq0,~x+y+t\leqq{3},~x+2t\leqq4,~y-t\leqq1$\
すなわち$\trenritu{0\leqq{x}\leqq4-2t\0\leqq{y}\leqq1+t\x+y\leqq{3-t}}$で表される領域である。\
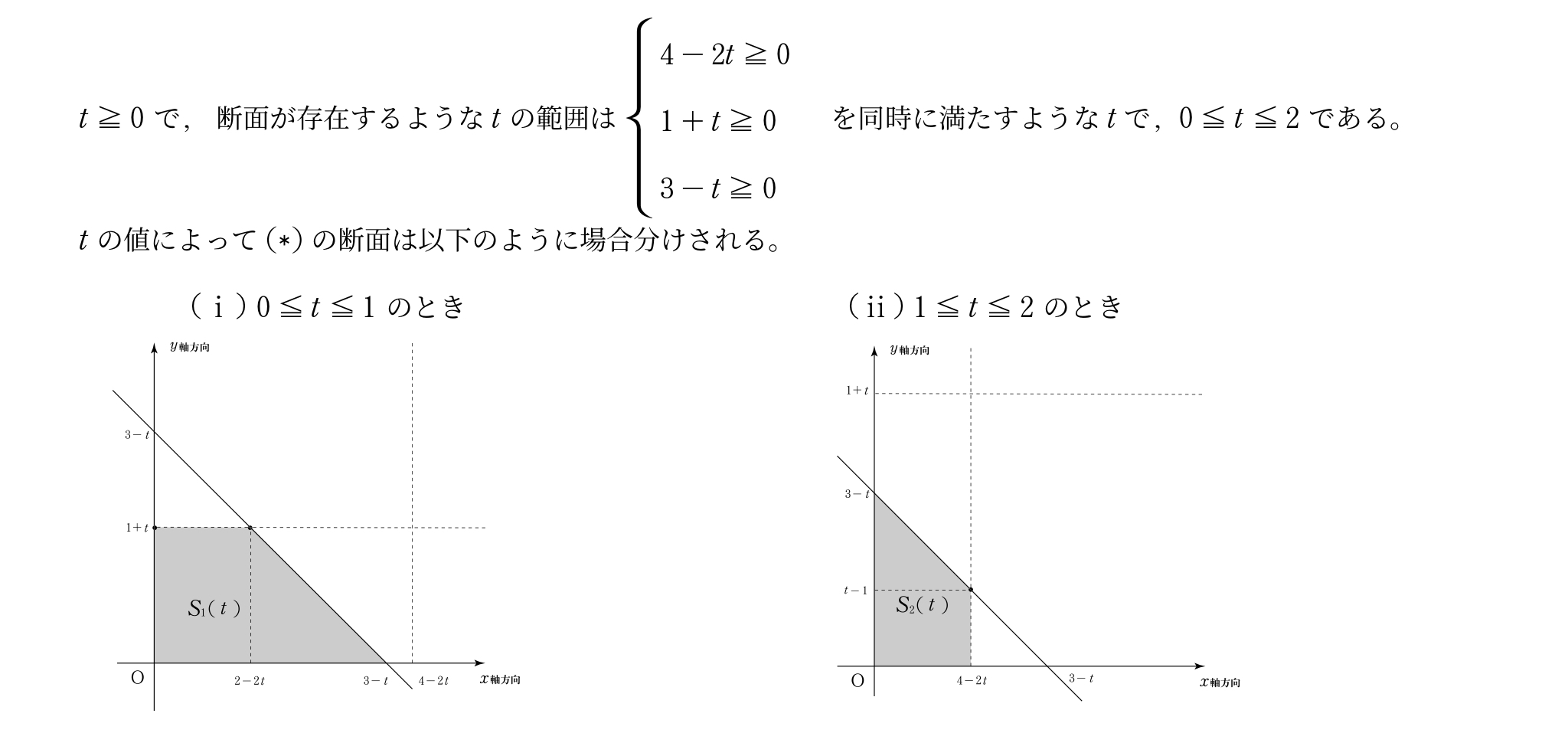
$t\geqq{0}$~で,断面が存在するような$t$の範囲は$\trenritu{4-2t\geqq{0}\1+t\geqq0\3-t\geqq0}$~を同時に満たすような$t$で,$0\leqq{t}\leqq{2}$~である。\
$t$の値によって$(\ast)$の断面は以下のように場合分けされる。\
\tokeiichi~$0\leqq{t}\leqq{1}$~のとき\tokeini~$1\leqq{t}\leqq{2}$~のとき
\tokeiichi~の場合の断面積を$S_1(t)$と名付けると
\tokeini~の場合の断面積を$S_2(t)$と名付けると
$S_2(t)=\bunsuu12\B{(t-1)+(3-t)}(4-2t)=4-2t$\
以上から立体$(\ast)$の体積は\
~~~~$\dint{0}{1}S_1(t)\,dt+\dint{1}{2}S_2(t)\,dt=$$\dint{0}{1}\p{-\bunsuu32t^2+t+\bunsuu52}\,dt+\dint{1}{2}(4-2t)\,dt$\
$=\bunsuu72\kotae$




コメント